3.1.1 Gravitational Force Between Two Bodies in The Universe
Revision Notes
Gravitational Force Between Two Bodies in The Universe
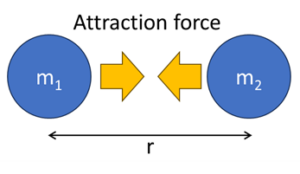
- The force of gravity is present among all objects in the universe.
- In Figure to the left, there are two objects with masses represented as \(m_1\) and \(m_2\).
- The distance between the two objects is denoted as \(r\).
- The gravitational force acting between these two objects is represented as \(F\).
- According to Newton’s theory:
The force of gravity, F, between two objects is directly proportional to the product of their masses.
\[
F \propto m_1 \times m_2–(1)
\] - This gravitational force, \(F\), is inversely proportional to the square of the distance between the objects’ centers.
\[
F \propto \frac{1}{r^2}–(2)
\] - By combining equations (1) and (2), we can derive the following relationship:
\[
F \propto \frac{m_1 \times m_2}{r^2}
\]
Then, we can express the gravitational force using the formula:
\[
F=G \frac{m_1 \times m_2}{r^2}
\]
where:
\(G\) represents the universal gravitational constant, which has a value of \(=6.67 \times 10^{-11} N m ^2 kg ^{-2}\).
This formula is known as Newton’s Law of Universal Gravitation. - According to Newton’s law of Universal Gravitation:
Every object in the universe attracts every other object with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. - The gravitational force between two objects can be calculated using the formula:
\[
F=G \frac{m_1 \times m_2}{r^2}
\]
Solving Problems involving Newton's Law of Universal Gravitation:
(I) Two bodies at rest on Earth
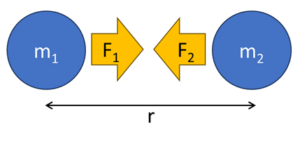
When two bodies, \(m_1\) and \(m_2\), are at rest on Earth’s surface and separated by a distance, \(r\), the magnitude of the gravitational force between them, \(F_1\) and \(F_2\), are equal in value and act in opposite directions.
Example
Determine the force of gravitational attraction between two adult of masses \(65 kg\) and \(85 kg\) respectively standing at \(2 m\) apart. [ \(G=6.67 \times 10^{-11} N m ^2 kg ^{-2}\) ]
Solution
\[
\begin{aligned}
m_1 & =65 kg \\
m_2 & =85 kg \\
r & =2 m \\
G & =6.67 \times 10^{-11} Nm ^2 kg ^{-2}
\end{aligned}
\]
\[
\begin{aligned}
F & =\frac{G m_1 m_2}{r^2} \\
& =\frac{\left(6.67 \times 10^{-11}\right)(65)(85)}{2^2} \\
& =9.21 \times 10^{-8} N
\end{aligned}
\]
Therefore, the gravitational attraction between the two students is calculated to be \(9.21 \times 10^{-8} N\).
This gravitational attraction is significantly smaller when compared to the students’ weights, which are \(650 N\) and \(850 N\) respectively. (Assuming the value of gravitational acceleration is \(10 m / s ^2\) ).
Summary:
- The force of gravity exists among all objects in the universe.
- Gravity becomes noticeable when dealing with large objects like Earth, Moon, Sun, and planets.
- Newton’s theory states that the gravitational force, \(F\), between two objects is proportional to the product of their masses \(\left(m_1\right.\) and \(\left.m_2\right)\) but inversely proportional to the square of the distance, \(r\), between the objects’ centers.
- Combining these relationships, we can express the gravitational force as \(F=\frac{G m_1 m_2}{r^2}\).
The Effect of Mass and Distance Between Two Bodies on Gravitational Force:
- According to the equation of Newton’s law of universal gravitation, \(F=\frac{G\left(m^1 m^2\right)}{r^2}\), there are two factors that influence the force of gravitational attraction between two bodies: mass \(( m )\) and the distance between their centers ( \(r\) ).
- If the mass of either object increases, the force of gravity between them also increases. On the other hand, if the distance between their centers increases, the force of gravity decreases.
(II) Body on Earth’s surface

- When an object is on the surface of the Earth, the force \((f)\) of gravity acting on the object is its weight(W).
- According to Newton’s law of universal gravitation, the force of gravitational attraction between the body and the Earth can be given by the formula:
\[
F=G \frac{M m}{R^2}
\]
Here, \(M\) represents the mass of the Earth, \(m\) represents the mass of the object, and \(R\) represents the distance between the center of the object and the center of the Earth. - It is important to note that the gravitational force between the Earth and an object on its surface is equivalent to the weight of the object, as per Newton’s law of universal gravitation.
Example
What is the magnitude of the gravitational force between the Earth and \(1 kg\) mass object on its surface?
[Mass of Earth, \(M=5.98 \times 10^{24} kg\);
\(G=6.67 \times 10^{-11} N m ^2 kg ^{-2}\);
Radius of Earth, \(\left.R=6.38 \times 10^6 m \right]\)
(III) Earth and Satellite
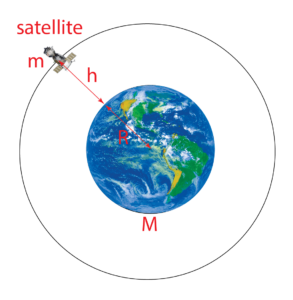
- Consider a satellite with mass \(m\) orbiting the Earth, which has a mass of \(M\) and a radius of \(r\).
- The satellite is located at a height of \(h km\) above the Earth’s surface.
- The gravitational force \((F)\) between the satellite and the Earth can be calculated using the formula:
\[
F=G \frac{M m}{(R+h)^2}
\]
Example:
A satellite with a mass of \(800 kg\) orbits around the Earth at a height of \(400 km\) above the surface of the Earth. Determine the gravitational force between the satellite and the Earth.
[The mass of the Earth is \(5.98 \times 10^{24} kg\), and the radius of the Earth is \(6.38 \times 10^6 m\).]
(IV) Earth and the Sun
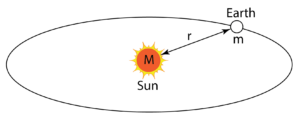
- Consider the interaction between the Earth and the Sun.
- We want to determine the gravitational force between the Earth and the Sun.
- Let’s denote the mass of the Earth as \(m\) (given as \(5.98 \times 10^{24} kg\) ) and the mass of the Sun as M (given as \(2 \times 10^{30} kg\) ).
- The average distance between the Earth and the Sun is denoted as \(r\) (given as \(1.5 \times 10^{11} m\) ).
- To calculate the gravitational force between the Earth and the Sun, we can use the formula:
\[
F=G \frac{M m}{R^2}
\]
Practice
- If a \(8.5 \times 10^4 kg\) mass and a \(4.5 \times 10^5 kg\) mass are separated by \(0.5 m\), determine the force of attraction between them.
- Two masses are put \(15 m\) apart, one of them being three times the other. \(0.5 N\) worth of force is felt. What is the mass of each object?
- How far away from the Moon’s surface will a spacecraft encounter zero net gravitational pull? [Distance between the centre of earth and moon \(=3.84 \times 10^8 m\); Radius of the moon \(=1.74 \times 10^6 m\); Mass of the moon \(=7.35 \times 10^{22} kg\). Mass of the earth \(=5.98 \times 10^{24} kg\) ]