3.1.2 Relationship between Gravitational Acceleration, (g) and Universal Gravitational Constant, G

1. The gravitational force on an object, \(m\) according to Newton’s Second Law of Motion, \(F=m g\).
2. The gravitational force between the object and the Earth according to Newton’s Law of Universal Gravitation,
   \[
   F=\frac{G M m}{r^2}
   \]
3. Equate both equations above,
   \[
   m g=\frac{G M m}{r^2}
   \]
   Thus, \(g=\frac{G M}{r^2}\)
   \(r=\) distance from the centre of the Earth,
   \(M=\) mass of the Earth
   Therefore,
   
   1. at the surface of the Earth, \(r=R\), hence
      \[
      g=\frac{G M}{R^2}
      \]
   2. at a position of height, \(h\) from the surface of the Earth, \(r=R+h\), hence
      \[
      g=\frac{G M}{(R+h)^2}
      \]
4. The graph below shows the variation of \(g\) with distance \(r\) from the centre of the Earth.
   
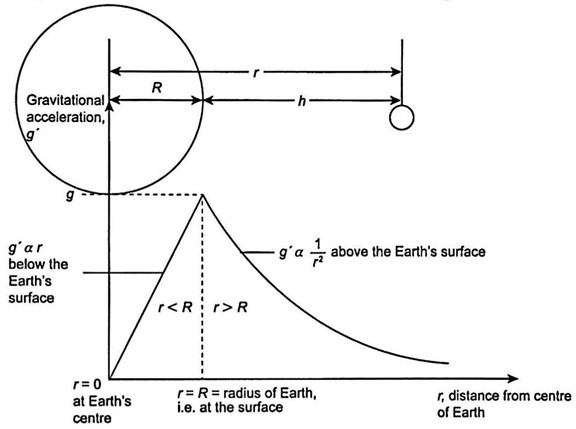
5. Based on Diagram 3.2,
   
   1. \(g\) is directly proportional to \(r, g \propto r\) if \(r<R\)
   2.  \(g\) is inversely proportional to \(r^2\),
      \(g \propto \frac{1}{r^2}\) if \(r \geq R\);
      \(R\) is radius of the Earth

Example

The mass of the Earth is \(5.97 \times\) \(10^{24} kg\) and the radius of the Earth is \(6.37 \times 10^6 m\). Calculate the gravitational acceleration at the surface of the Earth.
\[
\left[G=6.67 \times 10^{-11} N m ^2 kg ^{-2}\right]
\]

Solution
\[
\begin{array}{l}
M=5.97 \times 10^{24} kg , \\
R=6.37 \times 10^6 m , g=?
\end{array}
\]
Using formula \(g=\frac{G M}{r^2}\)
\[
\begin{aligned}
& \begin{array}{l}
\left(6.67 \times 10^{-11}\right) \times \\
\left(5.97 \times 10^{24}\right)
\end{array} \\
= & \frac{9.81 m s ^{-2}}{\left(6.37 \times 10^6\right)^2}
\end{aligned}
\]

Example

A satellite is orbiting the Earth at an altitude of \(460 km\). What is its gravitational acceleration at this altitude? [G \(=6.67 \times 10^{-11} N m ^2 kg ^{-2}\), mass of the Earth \(=5.97 \times 10^{24} kg\), radius of the Earth \(=6.37 \times 10^6 m\) ]
Solution
\[
\begin{array}{l}
\text { Height of orbit, } \begin{aligned}
h & =460 km \\
& =460000 m
\end{aligned} \\
\begin{aligned}
M & =5.97 \times 10^{24} kg , r=R+h, g=? \\
g & =\frac{G M}{r^2} \\
& =\frac{\left(6.67 \times 10^{-11}\right)\left(5.97 \times 10^{24}\right)}{\left[\left(6.37 \times 10^6\right)+460000\right]^2} \\
& =8.53 m s ^{-2}
\end{aligned}
\end{array}
\]

1. When the value of \(g\) on the surface of a planet is known, the magnitude of the gravitational force acting on an object on the surface of the planet can be calculated.
2. Knowledge of \(g\) plays an important role in space exploration and human survival.
3. Effect of gravity on the human body
   
   1. During space flight, the body works considerably less, causing muscle deterioration and loss of bone density. Upon returning to Earth, the muscle weakness causes pain.
   2. During space flight, fluids float up from the legs to the head causing puffy face and skinny legs. Upon returning to Earth, the astronauts might have difficulty on standing and might experience fainting due to rush of blood to the feet.
   3. Change in gravity causes uneven ventilation in the lung due to the deformation of lung tissue.
   4. During space flight, the eyes send signals that confuse the brain because the visual references for stability are missing. This may cause nausea and vomiting.
4. Effect of gravity on space exploration
   
   1. Scientists had to solve the problem of escaping from the Earth’s gravitational force that pulls objects towards the Earth and prevents them from floating off into space.
   2. A spacecraft leaving the Earth must travel fast enough to overcome this strong gravitational pull. The higher the value of gravitational acceleration on a planet means the higher the escape velocity required to overcome the gravitational pull. Thus, more fuel is required for the space exploration.