admin

Daya Paduan

by
  1. Paduan vektor ialah gabungan dua atau lebih vektor menjadi vektor tunggal yang boleh menggantikan vektor asal dan memberi kesan yang sama.
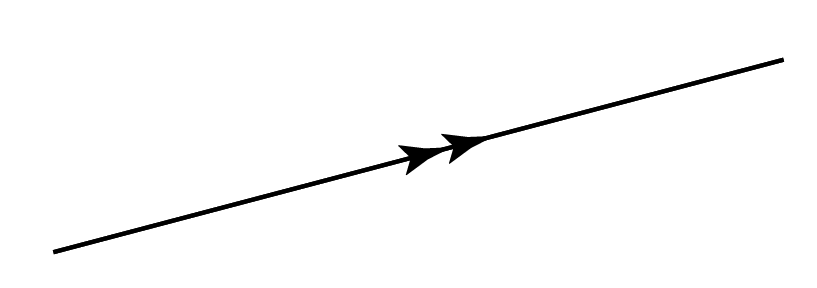
  2. Simbol untuk vektor paduan biasanya diwakili dengan dua anak panah yang sama dan sehala seperti yang ditunjukkan dalam Rajah di bawah.
  3. Penambahan dan penolakan. vektor tidak boleh dihitungkan seperti yang dilakukan. bagi kuantiti skalar
  4. Ini adalah kerana vektor ialah kuantiti yang mempunyai arah manakala kuantiti skalar tiada.

Paduan Vektor – Kaedah Segitiga



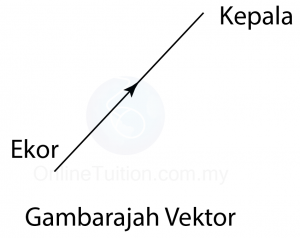
Untuk melakukan paduan vektor kaedah segitiga, sambungkan ekor bagi vektor yang kedua kepada kepala vektor pertama seperti ditunjukkan di dalam rajah di atas. Vektor berwarna merah ialah vektor paduan terbentuk.

Paduan Vektor – Kaedah Segiempat Selari


Untuk melakukan paduan vektor kaedah segiempat selari, sambungkan ekor bagi vektor pertama kepada ekor vektor pertama seperti ditunjukkan di dalam rajah di atas. Vektor berwarna merah ialah vektor paduan terbentuk.


Paduan Dua Vektor Berserenjang


Bagi vektor yang berserenjang, magnitud vektor boleh ditentukan dengan menggunakan teorem Pythagoras manakala arah vektor boleh ditentukan dengan menggunakan kaedah trigonometri seperti ditunjukkan di bawah:


Contoh:
Dua daya, P dan Q yang bermagnitud 10N dan 12N adalah berserenjang antara satu sama lain. Apakah magnitud daya paduan bagi kedua-dua daya itu apabila daya-daya itu dikenakan ke atas satu objek?

Jawapan:
Magnitud daya paduan
|F|= 10 2 + 12 2 =15.62N

Contoh:

Rajah di atas menunjukkan 4 daya yang bemagnitud 2N, 4N, 5N dan 8N dikenakan ke atas titik O. Semua daya ini adalah berserenjang antara satu sama lain. Berapakah magnitud daya paduan yang dikenakan ke atas titik O.

Jawapan:
Komponen mengufuk daya paduan terbentuk = 5 – 2 = 3N ke kanan
Komponen menegak daya paduan terbentuk =  8 – 4 = 4N ke bawah

Oleh itu, magnitud daya paduan bagi kedua-dua komponen ini,

|F|= 3 2 + 4 2 =5N


Kuantiti Vektor

by

Kuantiti Skalar dan Kuantiti Vektor

  1. Semua kuantiti fizik boleh dibahagi kepada dua jenis, iaitu
    1. Kuantiti Skalar
    2. Kuantiti Vektor
  2. Kuantiti skalar ialah kuantiti yang mempunyai magnitud sahaja seperti panjang, jarak, jisim, laju, kerja, dan sebagainya.
  3. Kuantiti vektor ialah kuantiti yang mempunyai magnitud dan arah seperti sesaran, halaju, momentum, daya, dan sebagainya.

Gambarajah Vektor

  1. Vektor biasanya diwakili oleh satu garis yang berarah.
  2. Panjang garis itu adalah magnitud vektor dan arah anak panah pula ialah arah vektor.
  3. Magnitud untuk sesuatu vektor misalnya vektor AB ditulis sebagai $v = {s \over t}$ $v = \frac{s}{t}$

Vektor Sama

  1. Dua vektor dikatakan sama jika kedua-duanya mempunyai magnitud dan arah yang sama.
  2. Dua vektor yang sama tidak semestinya bermula dan berakhir pada titik yang sama.

Vektor Negatif

Vektor negatif ialah vektor yang bermagnitud sama tetapi bertentangan arah dengan vektor yang dirujukkan.

Menentukan Pecutan daripada Pita Detik

by

Mencari Pecutan

Pecutan suatu gerakan dapat ditentukan oleh jangka masa detik dengan menggunakan persamaan berikut:
\[{a = \frac{{v – u}}{t}}\]
a = pecutan
v = halaju akhir
u = halaju awal
t = masa

Berjaga-jaga!
t ialah masa yang diambil oleh perubahan halaju dari halaju awal ke halaju akhir.

Contoh:

Pita detik di dalam rajah di atas dihasilkan oleh sebuah kereta mainan yang bergerak di atas satu landasan condong. Jika jangka masa detik yang digunakan menghasilkan 50 titik dalam satu saat, kira pecutan kereta mainan itu.

Jawapan:
Untuk mencari pecutan, kita perlu menentukan halaju awal, halaju akhir dan masa yang diambil oleh perubahan halaju berkenaan.Halaju awal,

\[\begin{array}{l}
u = \;\frac{s}{t}\;\;\\
= \;\frac{{3cm}}{{0.02s}}\;\; = 150cm\;s{\;^{ – 1}}
\end{array}\]

v= s t = 0.5cm 0.02s =25cm s −1

Masa yang diambil oleh perubahan halaju,
t = (0.5 + 4 + 0.5) ticks = 5 ticks
t = 5 × 0.02s = 0.1s

Pecutan,

a= v−u t a= 25−150 0.1 =−1250cm s −1

Contoh:

Sebuah troli ditolak menaiki satu cerun. Rajah di atas menunjukkan carta pita detik yang menunjukkan gerakan troli itu. Dalam carta itu, setiap keratan pita detik terdiri daripada 5 detik. Jika jangka masa detik itu menghasilkan 50 titik dalam satu saat, tentukan pecutan troli itu.

Jawapan:
Untuk mencari pecutan, kita perlu menentukan halaju awal, halaju akhir dan masa yang diambil oleh perubahan halaju berkenaan.Halaju awal,

u= s t = 5cm 0.1s =50cm s −1

Halaju akhir

v= s t = 1cm 0.1s =10cm s −1

Masa yang diambil oeleh perubahan halaju,
t = (2.5 + 5 + 5 + 5 + 2.5) ticks = 20 ticks
t = 20 × 0.02s = 0.4s

Pecutan,

a= v−u t a= 10−50 0.4 =−100cm s −1

Menentukan Halaju daripada Pita Detik

by

Mencari Halaju
Halaju suatu gerakan boleh ditentukan dengan menggunakan pita detik dengan persamaan berikut:
\[v = \frac{s}{t}\]
v = halaju
s = sesaran
t = masa 

Berjaga-jaga!
t ialah masa dari titik pertama ke titik terakhir bagi jarak yang diukur.

Contoh:

Rajah di atas menunjukkan sekerat pita detik yang ditarik melalui satu jangka masa detik yang bergetar 50 kali dalam satu saat. Berapakah
a. masa yang diambil dari titik pertama ke titik terakhir dalam pita detik ini?
b. halaju purata bagi pergerakan ini?
Jawapan:
a.
Terdapat 15 detik di antara titik pertama dan titik terakhir, makaMasa yang diambil = 15 × 0.02s = 0.3s

b. Jarak yang dilalui = 15cm

\[\begin{array}{l}
v = \frac{s}{t}\\
v = \frac{{15}}{{0.3}} = 50cm{s^{ – 1}}
\end{array}\]

Ciri-ciri Penting Keselamatan Kenderaan

by

Zon Remuk

Zon remuk meningkatkan masa tindakbalas perlanggaran semasa berlakunya kemalangan.
Ini menyebabkan daya impuls dikurangkan seterusnya menurunkan risiko kecederaan.

Tali Pinggang Keledar


Menghalang penumpang daripada terhumban ke hadapan atau keluar ke kenderaan apabila kenderaan dihentikan dengan mendadak.

Beg Udara Automatik


Semasa berlakunya kemalangan, beg udara mengembang dan bertindak sebagai kusyen untuk mengurangkan daya impuls jika penumpang terhumban ke hadapan.

Penyandar Kepala

Mengurangkan kederaan leher pemandu atau penumbang terhumban ke belakang apabila kereta dilanggar dari belakang.

Cermin Anti Pecah dan Berselerak

Cermin anti pecah dan berselerak digunakan sebagai cermin depan kenderaan supaya ia tidak pecah kepada serpihan kecil jika berlakunnya kemalangan. Ini mengurangkan kecederaan yang disebabkan oleh serpihan kaca yang berselerak.

Dashboard Beralas Bahan Lembut

Dashboard ditutupi dengan bahan lembut. Ini dapat memanjangkan masa tindakbalas dan seterusnya mengurangkan daya impuls apabila penumpang terhentak ke atasanya.

Collapsible Steering Columns

The steering will swing away from driver’s chest during collision. This may reduce the impulsive force acting on the driver.

Sistem Mencegah Brek Terkunci (ABS)

Mengelakkan keperluan mengepam brek apabila hendak berhenti dengan tiba-tiba dan seretusnya mencegah
roda dari terkunci dan kereta tergelongsor.

Bumper

Diperbuat daripada bahan kenyal supaya ia boleh menyerap hentakan yang kecil apabila berlakunya perlanggaran.

Ruang Keselamatan Penumpang

Badan kereta dibuat daripada keluli yang kuat dan tidak medah remuk.
Ini dapat mengelakkan penumpang daripada terkena daya dari luar secara terus.

Kesan Masa Ke Atas Magnitud Daya Impuls

by

Contoh-contoh yang melibatkan daya impuls

  1. Lompat jauh
  2. Lompat tinggi
  3. Bermain bola sepak
  4. bermain badminton
  5. bermain bola tenis
  6. bermain golf
  7. bermain besbol

Lompat Jauh

  1. Tambak lompat jauh diisi dengan pasir. Ini adalah untuk memanjangkan masa tindak balas dan seterusnya mengurangkan daya impuls yang dikenakan ke atas kaki atlit apabila mereka mendarat di atasnya.

Lompat Tinggi


(This image is licenced under the GNU Free Document Licence. The original file is from the Wikipedia.org.)

  1. Dalam acara lompat tinggi, peserta-peserta akan jatuk ke atas satu tilam yang tebal dan lembut selepas lompatan.
  2. Ini adalah untuk meningkatkan masa tindak balas dan seterusnya mengurangkan daya impuls yang dikenakan ke atas badan para peserta untuk mengelakan kecederaan.

    Melompat dan Mendarat Dari Tempat Tinggi

    1. Seseorang akan membengkkokkan kakinya semasa mendarat apabila melompat dari tempat tinggi.
    2. Ini adalah untuk memanjangkan masa tindak balas dan seterusmnya mengurangkan hentakan daya impuls yang dikenkan ke atas kaki pelompat.

    Impuls dan Daya Impuls

    by

    Impuls

    1. Hasil darab daya F dengan masa tindakannya t dikenali sebagai impuls suatu daya.
      Impuls = Ft
    2. Impuls yang dikenakan ke atas suatu objek adalah sama dengan perubahan momentum objek itu.
      Impuls = perubahan momentum = mv – mu
    3. Impuls ialah kuantitik vektor.

    Contoh:
    Sebiji bola besi berjisim 0.4kg berada dalam keadaan pegun di atas meja yang licin. Bola itu kemudian diberi satu impuls sebanyak 5.0 Ns secara mendatar. Berapakah halaju bola itu selepas tindakan itu?

    Jawapan:
    Impuls = mv – mu
    (5.0) = (0.4)v – (0.4)(0)
    0.4v = 0.5
    v = 1.25 m/s

    Halaju bola selepas tindakan = 1.25 m/s

    Daya Impuls

    1. Daya impuls ditakrifkan sebagai kadar perubahan momentum terhadap masa tindakan yang singkat bagi suatu objek yang bergerak. Secara matematik, ini ditulis sebagai
    2. Ia adalah daya yang dikenakan ke atas suatu objek dalam jangka masa yang singkat semasa perlanggaran atau letupan.

    Contoh:
    Sebuah kereta berjisim 1000kg bergerak dengan halaju 25 m/s. Kereta itu melanggar  tiang lampu jalan dan berhenti dalam masa 0.05 saat. Berapakah daya impuls yang dikenakan ke atas kereta itu dalam perlanggaran ini.

    Jawapan:
    m = 1000kg
    u = 24 m/s
    v = 0
    t = 0.05s


    Kesan Tindakan Impuls/ Daya Impuls

    1. Daya yang dikenakan ke atas suatu objek menentukan pecutan objek itu. Semakin besar daya itu, semakin tinggi pecutan objek itu.
    2. Impuls yang dikenkan ke atas suatu objek pula menentukan perubahan halaju objek itu. Semakin besar impuls yang dikenakan, semakin besar perubahan halaju objek yang dialami oleh objek itu.

      Hukum Gerakan Newton Ketiga

      by

      Hukum Newton ketiga menyatakan bahawa,

      jika satu objek P mengenakan satu daya, F ke atas satu objek yang lain, maka objek itu akan mengenakan satu daya tindak balas yang mempunyai magnitud yang sama tetapi pada arah yang bertentangan, iaitu -F ke atas objek A.

      Ini bermakna, setiap tindakan daya akan menghasilkan satu daya tindak balas yang mempunyai minat yang sama dalam arah yang bertentangan.

      Contoh 1:

      Apabila seorang itu menolak dinding dengan satu daya F, dinding itu akan menghasilkan satu daya tindak balas -F. Oleh kerana kedua-dua daya ini mempunyai magnitud yang sama tetapi bertindak dalam arah yang bertentangan, maka lelaki itu adalah adalah dalam keseimbangan daya.

      Contoh 2:
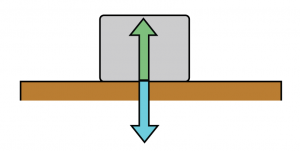      Satu bongkah diletak di atas meja. Berat bongkah itu akan mengenakan satu daya W ke atas permukaan meja. Mengikut Hukum Newton Ketiga, satu daya yang bermagnitud |W| tetapi dalam arah yang bertentangan akan dihasilkan.

      Ringkasan 3 Hukum Gerakan Newton

      Hukum Gerakan Newton Kedua

      by

      Hukum Newton Kedua

      Hukum Gerakan Newton Kedua menyatakan bahawa kadar perubahan momentum adalah berkadar terus dengan daya paduan yang bertindak ke atas objek itu pada arah yang sama dengan arah tindakan daya paduan itu. Implikasi: Apabila terdapat satu daya paduan yang bukan sifar dikenakan ke atas satu objek, objek itu akan memecut (lajunya bertambah/berkurang atau arah gerakannya berubah). Formula bagi Daya \[F = ma\] F = Daya bersih m = jisim objek a = pecutan (PENTING: F mestilah daya bersih)
      Ringkasan Hukum Newton Pertama dan Kedua
      Hukum Newton Pertama: Apabila tiada daya bersih dikenakan ke atas satu objek, objek itu sama ada dalam keadaan pegun atau bergerak dalam garis lurus dengan laju malar. Hukum Newton Kedua: Apabila terdapat daya bersih dikenakan ke atas satu objek, objek itu akan memecut.

      Contoh:
      Sebuah kotak berjisim 150kg diletakkan di atas satu lantai licin yang mendatar. Cari pecutan yang dialami oleh kotak itu jika satu daya 300N dikenakan ke atas kotak itu secara mengufuk.
      Jawapan:
      F = ma
      (300) = (150)a
      a = 2 ms-2

      Contoh:
      Satu objek berjisim 50kg diletakkan di atas satu lantai mendatar dan licin. Jika halaju objek itu berubah daripada pegun kepada 25.0 m/s dalam 5 saat apabila dikenakan satu daya F secara mengufuk. Berapakah magnitud daya F?Jawapan:
      Daya dapat dihitung dengan menggunakan formula F = ma. Jisim m objek telah diberi dalam soalan. Bagaimanapun, pecutan, a, tidak diberi terus.

      Kita boleh menentukan pecutan a dengan menggunakan formula

      \[\begin{array}{*{20}{l}}
      {a = \frac{{v – u}}{t}}\\
      {a = \frac{{25 – 0}}{5} = 5m{s^{ – 2}}}
      \end{array}\]
      Daripada formula
      F = ma = (50)(5) = 250N

      Daya yang dikenakan ke atas objek itu ialah 250N.

      Kesimpulan

      1. Jika terdapat daya bersih bertindak ke atas satu jasad, jasad itu akan mengalami pecutan. ( Pecutan ini mungkin ialah pertambahan halaju, pengurangan halaju atau perubahan arah pergerakan. ).
      2. Semakin tinggi daya dikenakan, semakin tinggi pecutan dialami oleh jasad itu.
      3. Semakin besar jisim jasad itu, semakin rendah pecutan yang dialami. Ini bermakna, jisim merupakan rintangan (halangan) kepada pergerakan.

      Daya

      by
      1. Daya ialah tolakan atau tarikan yang dikenakan ke atas satu objek.
      2. Daya ialah kuantiti vektor yang mempunyai magnitud dan arah.
      3. Unit daya ialah Newton (atau kgms-2).

      Daya tidak Seimbang/ Daya Paduan

      1. Jika daya-daya yang dikenakan ke atas suatu objek adalah tidak seimbang, maka wujudlah satu daya bersih yang bertindak ke atas objek itu. Daya bersih itu dikenali sebagai daya paduan.
      2. Daya yang dikenakan ke atas satu objek boleh mengubah 
        1. saiz,
        2. bentuk,
        3. keadaan rehat,
        4. halaju, dan
        5. arah gerakan
        6. objek itu.