Example 2:
An iron block which has volume 0.3m³ is immersed in water. Find the upthrust exerted on the block by the water. [Density of water = 1000 kg/m³]
Answer:
Density of water, ρ = 1000 kg/m³
Volume of water, V = 0.3 m³
Gravitational Field Strength, g = 10 N/kg
Upthrust, F = ?
F = ρVg
F = (1000)(0.3)(10)
F = 3000N
Example 3:
The figure above shows an empty boat floating at rest on the water. Given that the mass of the boat is 150kg. Find
- the upthrust acting on the boat.
- The mass of the water displaced by the boat.
- The maximum mass that the boat can load safely if the volume of the boat at the safety level is 3.0 m³.
Answer:
a. According to the principle of flotation, the upthrust is equal to the weight of the boat.
Upthrust,
F = Weight of the boat
= mg
= (150)(10)
= 1500N
b. According to the Archimedes’ Principle, the weight of the water displaced = Upthrust
Weight of the displaced water,
W = mg
(1500) = m(10)
m = 150kg
c.
Maximum weight can be sustained by the boat
F=ρVg
F=(1000)(3)(10)
=30,000N
Maximum weight of the load
= Maximum weight sustained – Weight of the boat
= 30,000 – 1,500 = 28,500N
Maximum mass of the load
= 28500/10 = 2850 kg
In figure above, a cylinder is immersed in water. If the height of the cylinder is 20cm, the density of the cylinder is 1200kg/m³ and the density of the liquid is 1000 kg/m³, find:
a. The weight of the object
b. The buoyant force
Answer:
a.
Volume of the cylinder, V = 50 x 20 = 1000cm³ = 0.001m³
Density of the cylinder, ρ = 1200 kg/m³
Gravitational Field Strength, g = 10 N/kg
Weight of the cylinder, W = ?
W=ρVg W=(1200)(0.001)(10)=12N
b.
Volume of the displaced water = 50 x 12 = 600cm³ = 0.0006m³
Density of the water, ρ = 1000 kg/m³
Upthrust, F = ?
F=ρVg F=(1000)(0.0006)(10)=6N
The density and mass of a metal block are 5.0×103 kg m-3 and 4.0kg respectively. Find the upthrust that act on the metal block when it is fully immerse in water.
[ Density of water = 1000 kgm-3 ]
Answer:
In order to find the upthrust, we need to find the volume of the water displaced. Since the block is fully immersed in water, hence the volume of the water displaced = volume of the block.
Volume of the block,
V= m ρ = 4 5.0× 10 3 =0.0008 m 3
Upthrust acted on the block,
F=ρVg F=(1000)(0.0008)(10)=8N
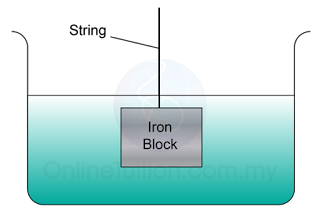
A metal block that has volume of 0.2 m³ is hanging in a water tank as shown in the figure to the left. What is the tension of the string? [ Density of the metal = 8 × 10³ kg/m³, density of water = 1 × 10³ kg/m³]
Answer:
Let,
Tension = T
Weight = W
Upthrust = F
Diagram below shows the 3 forces acted on the block.
The 3 forces are in equilibrium, hence
T+F=W T=W−F T= ρ 1 Vg− ρ 2 Vg T=( ρ 1 − ρ 2 )Vg =(8000−1000)(0.2)(10)=14,000N
Video
A wooden sphere of density 0.9 g/cm³ and mass 180 g, is anchored by a string to a lead weight at the bottom of a vessel containing water. If the wooden sphere is completely immersed in water, find the tension in the string.
Answer:
Let’s draw the diagram that illustrate the situation:
We need to determine the volume of the displaced water to find the upthrust.
Let the volume of the wooden sphere = V
V= m ρ = 180 0.9 =200c m 3
Let,
Tension = T
Weight = W
Upthrust = F
All the 3 forces are in equilibrium, hence
T+W=F T=F−W T= ρ 1 Vg− ρ 2 Vg T=( ρ 1 − ρ 2 )Vg =(1000−800)(0.0002)(10)=0.4N
Figure above shows a copper block rest on the bottom of a vessel filled with water. Given that the volume of the block is 1000cm³. Find the normal reaction acted on the block.
[Density of water = 1000 kg/m³; Density of copper = 3100 kg/m³]
Answer:
Volume of the block, V = 1000cm³ = 0.001m³
Let,
Normal Reaction = R
Weight = W
Upthrust = F
Diagram below shows the 3 forces acted on the block.
All the 3 forces are in equilibrium, hence
R+F=W R=W−F R= ρ 1 Vg− ρ 2 Vg R=( ρ 1 − ρ 2 )Vg =(3100−1000)(0.001)(10)=21N