Force and Pressure – OnlineTuition.com.my

Archimedes Principle – Structure Question 3

by admin

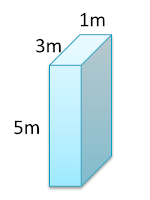
A balloon filled with helium gas has negligible mass. The volume of the balloon is 120cm³. [Density of air = 1.23 kg/m³.Density of helium gas = 0.18 kg/m³]

Calculate the mass of the helium gas in the balloon?

m=ρV m=(0.18)(120× 10 −6 )=2.16× 10 −5 kg

Find the weight of the helium gas?
W=mg W=(2.16× 10 −5 )(10)=2.16× 10 −4 N

The balloon is then tied to a load of mass m kg, as shown in figure above. The balloon and the load float in the air stationary.

Mark in the diagram, all the forces that acted on the balloon.

Write an equation to relate all the forces in )b) (i).
All the 3 forces are in equilibrium

Upthrust = Weight of the Load + Weight of Helium Gas

Calculate the mass of the load, m.

Upthrust = Weight of the Load + Weight of Helium Gas ρVg=mg+2.16× 10 −4 (1.23)(120× 10 −6 )(10)−2.16× 10 −4 =m(10) m=1.26× 10 −4 kg

If the string that is tied to the balloon is cut, Find upward acceleration experienced by the balloon?
Net force acted on the balloon = mg = (1.26 x 10^-4)(10) = 1.26 x 10^-3N
Mass of the helium gas, m = 2.16 x 10^-5kg

F=ma (1.26× 10 −3 )=(2.16× 10 −5 )a a= 1.26× 10 −3 2.16× 10 −5 =58.3m s −2

Archimedes Principle – Structure Question 2

by admin

Figure above shows a glass tube with cross-sectional area of 10 cm² and mass 10 g. It is filled with lead shots and immerse in water. The tube floats upright in the water. [Density of water is 10 g/cm³]

State the name of this device.
Hydrometer

State one use of this device in a laboratory.
To measure the density of liquids.

Explain the function of the lead shots in the glass tube?
To lower down the centre of gravity of the glass tube so that it does not topple when immerse in water.

The length of the glass tube immerse in water is 12 cm. Calculate

the volume of water displaced by the glass tube
A = 10 cm²
h = 12 cm
Let the volume of water = V
V = hA = (12)(10) = 120 cm³
the weight of the displaced water.
Mass of the displaced water = 120g = 0.12 kg
Weight of the displaced water = mg = 0.12 x 10 = 1.2 N

The glass tube together with the lead shots are then placed inside a container that filled with cooking oil. Again, the tube floats upright.

What can be observed in the part of tube that is immerse in the oil when compared with the condition in figure above?
Longer

Explain your answer in (b)(i).
The density of the oil is lower than the water.
Therefore, the volume of oil displaced is greater than the volume of the water displaced to produce the upthrust of same magnitude.

Archimedes Principle – Structure Question 1

by admin

Diagram (a) above shows a metal block supported by a spring balance. Diagram (b) shows the block partially immerses in water while diagram (c) shows the block fully immerses in water.

What is the mass of the metal block?
W = mg
(20) = m(10)
m = 2kg
In diagram b), the reading of the balance became 14N.

What is the effective weight loss of the block when partially immense in water as shown in diagram (b)?

Weight loss = 20 – 14 = 6N

What is the value of the upthrust that act on the block?

6 N

Find the weight of the displaced water?

6 N

In diagram c), when the block is fully immerse in water, the reading of the spring balance became 10N.

Name 3 forces that acted on the block.
Weight, tension of the string, upthrust

State and explain the relationship between the forces in (c) (i)
Both the tension and the upthrust act upward, the weight acts downward. The block doesn’t move. Therefore, all forces are in equilibrium.
Weight = Tension of the String + Upthrust

Find the volume of the block. [Density of water = 1000 kg m-3]
Mass of the displaced water = 1 kg

Name the principle you used in the calculation in question (c) (iii).
Archimedes’ Principle

What will happen to the reading of the spring balance if the water is replaced with cooking oil.
Increase

Explain your answer in (c) (v)
The upthrust produced is directly proportional to the density.
The cooking has lower density. Therefore the upthrust produced is lower. As a result, the weight loss caused by the upthrust will decrease and the reading of the spring balance will increase.

Archimedes Principle – Example 1

by admin

Example 1:
Determine the upthrust acted on the objects immerse in the water below.
a.

Answer:
a. Upthrust = Weight of the displaced water = 15N

b. Upthrust = Weight of the displaced water = 32N

c. Upthrust = Weight of the displaced water = 20N

Example 2:
An iron block which has volume 0.3m³ is immersed in water. Find the upthrust exerted on the block by the water. [Density of water = 1000 kg/m³]

Answer:

Density of water, ρ = 1000 kg/m³
Volume of water, V = 0.3 m³
Gravitational Field Strength, g = 10 N/kg
Upthrust, F = ?

F = ρVg
F = (1000)(0.3)(10)
F = 3000N

Example 3:

The figure above shows an empty boat floating at rest on the water. Given that the mass of the boat is 150kg. Find

the upthrust acting on the boat.
The mass of the water displaced by the boat.
The maximum mass that the boat can load safely if the volume of the boat at the safety level is 3.0 m³.

Answer:
a. According to the principle of flotation, the upthrust is equal to the weight of the boat.

Upthrust,
F = Weight of the boat
= mg
= (150)(10)
= 1500N

b. According to the Archimedes’ Principle, the weight of the water displaced = Upthrust

Weight of the displaced water,
W = mg
(1500) = m(10)
m = 150kg

c.
Maximum weight can be sustained by the boat

F=ρVg
F=(1000)(3)(10)
=30,000N

Maximum weight of the load
= Maximum weight sustained – Weight of the boat
= 30,000 – 1,500 = 28,500N

Maximum mass of the load
= 28500/10 = 2850 kg

Example 4:

In figure above, a cylinder is immersed in water. If the height of the cylinder is 20cm, the density of the cylinder is 1200kg/m³ and the density of the liquid is 1000 kg/m³, find:
a. The weight of the object
b. The buoyant force

Answer:
a.
Volume of the cylinder, V = 50 x 20 = 1000cm³ = 0.001m³
Density of the cylinder, ρ = 1200 kg/m³
Gravitational Field Strength, g = 10 N/kg
Weight of the cylinder, W = ?

W=ρVg W=(1200)(0.001)(10)=12N
b.
Volume of the displaced water = 50 x 12 = 600cm³ = 0.0006m³
Density of the water, ρ = 1000 kg/m³
Upthrust, F = ?
F=ρVg F=(1000)(0.0006)(10)=6N

Example 5
The density and mass of a metal block are 5.0×10³ kg m^-3 and 4.0kg respectively. Find the upthrust that act on the metal block when it is fully immerse in water.
[ Density of water = 1000 kgm^-3 ]

Answer:
In order to find the upthrust, we need to find the volume of the water displaced. Since the block is fully immersed in water, hence the volume of the water displaced = volume of the block.

Volume of the block,
V= m ρ = 4 5.0× 10 3 =0.0008 m 3
Upthrust acted on the block,
F=ρVg F=(1000)(0.0008)(10)=8N

Example 6:

A metal block that has volume of 0.2 m³ is hanging in a water tank as shown in the figure to the left. What is the tension of the string? [ Density of the metal = 8 × 10³ kg/m³, density of water = 1 × 10³ kg/m³]

Answer:
Let,
Tension = T
Weight = W
Upthrust = F

Diagram below shows the 3 forces acted on the block.

The 3 forces are in equilibrium, hence
T+F=W T=W−F T= ρ 1 Vg− ρ 2 Vg T=( ρ 1 − ρ 2 )Vg =(8000−1000)(0.2)(10)=14,000N

Video

Example 7:
A wooden sphere of density 0.9 g/cm³ and mass 180 g, is anchored by a string to a lead weight at the bottom of a vessel containing water. If the wooden sphere is completely immersed in water, find the tension in the string.

Answer:
Let’s draw the diagram that illustrate the situation:

We need to determine the volume of the displaced water to find the upthrust.
Let the volume of the wooden sphere = V
V= m ρ = 180 0.9 =200c m 3
Let,
Tension = T
Weight = W
Upthrust = F

All the 3 forces are in equilibrium, hence
T+W=F T=F−W T= ρ 1 Vg− ρ 2 Vg T=( ρ 1 − ρ 2 )Vg =(1000−800)(0.0002)(10)=0.4N

Example 8:

Figure above shows a copper block rest on the bottom of a vessel filled with water. Given that the volume of the block is 1000cm³. Find the normal reaction acted on the block.
[Density of water = 1000 kg/m³; Density of copper = 3100 kg/m³]

Answer:
Volume of the block, V = 1000cm³ = 0.001m³

Let,
Normal Reaction = R
Weight = W
Upthrust = F

Diagram below shows the 3 forces acted on the block.

All the 3 forces are in equilibrium, hence
R+F=W R=W−F R= ρ 1 Vg− ρ 2 Vg R=( ρ 1 − ρ 2 )Vg =(3100−1000)(0.001)(10)=21N

Simple Mercury Barometer – Example 1

by admin

Converting the Unit from cmHg to Pa

Pressure in unit cmHg can be converted to Pa by using the formula

P = hρg

Example 1:

Find the pressure at point A, B, C, D, D, E and F in the unit of cmHg and Pa. [Density of mercury = 13600 kg/m³]

Answer:

Pressure in unit cmHg	Pressure in unit Pa
P_A = 0 P_B = 17 cmHg P_C = 17 + 59 = 76 cmHg P_D = 76 + 8 = 84 cmHg P_E = 76 cmHg P_F = 76 cmHg	P_A = 0 P_B = hρg = (0.17)(13600)(10) = 23,120 Pa P_C = hρg = (0.76)(13600)(10) = 103,360 Pa P_D = hρg = (0.84)(13600)(10) = 114,240 Pa P_E = hρg = (0.76)(13600)(10) = 103,360 Pa P_F = hρg = (0.76)(13600)(10) = 103,360 Pa

Example 2:

Figure above shows a simple mercury barometer. What is the value of the atmospheric pressure shown by the barometer? [Density of mercury = 13600 kg/m³]

Answer:
Atmospheric Pressure,

P = 76 cmHg

or

P = hρg = (0.76)(13600)(10) = 103360 Pa

Example 3:

In above, the height of a mercury barometer is h when the atmospheric pressure is 101 000 Pa.
What is the pressure at X?

Answer:
Atmospheric Pressure,
P_atm = h cmHg = 101 000 Pa

Pressure at X,
P_X = (h – ¼h) = ¾h cmHg

P_X = ¾ x 101 000 = 75 750 Pa

Example 4:

Figure above shows a mercury barometer whereby the atmospheric pressure is 760 mm Hg on a particular day. Determine the pressure at point
a. A,
b. B,
c. C.
[Density of Mercury = 13 600 kg/m³]
Answer:
a.

P_A = 0

P_B = 50 cmHg

P_B = hρg = (0.50)(13600)(10) = 68 000 Pa

P_C = 76 cmHg

P_C = hρg = (0.76)(13600)(10) = 103 360 Pa

Example 6:
If the atmospheric pressure in a housing area is 100 000 Pa, what is the magnitude of the force exerted by the atmospheric gas on a flat horizontal roof of dimensions 5m × 4m?

Answer:
Area of the roof = 5 x 4 = 20 m²

Force acted on the roof

F = PA
F = (100 000)(20)
F = 2,000,000 N

Example 5:

Figure above shows a simple barometer, with some air trapped in the tube. Given that the atmospheric pressure is equal to 101000 Pa, find the pressure of the trapped gas. [Density of Mercury = 13 600 kg/m³]

Answer:
Pressure of the air = Pair
Atmospheric pressure = Patm

Pair + 55 cmHg = Patm

Pair
= Patm – 55 cmHg
= 101 000 – (0.55)(13 600)(10)
= 101 000 – 74 800
= 26 200 Pa

Example 7:

Figure(a) above shows the vertical height of mercury in a mercury barometer in a laboratory. Figure(b) shows the mercury barometer in water at a depth of 2.0 m.

Find the vertical height (h) of the mercury in the barometer in the water. Given that the pressure at a depth of 10 m from the water surface is 75 cmHg. [Density of water = 1000 kg/m³, Density of mercury = 13 600 kg/m³]

Answer:
Atmospheric pressure,
P_atm = 75 cmHg

Pressure caused by the water,
P_water = 2/10 x 75 = 15cmHg

Pressure in 2m under water
= 75 + 15 = 90 cmHg

Vertical height of the mercury = 90cm

Applications of Low Pressure

by admin

The examples of application of low pressure are

Foundation of Building

Snow Shoes

Ski Board

Tyre of Tractor

Feet of Elephant

Strip of Handbag

Seat Belt

Applications of High Pressure

by admin

The examples of application of high pressure are:

Sharp Knife

Ice-Skate

Sole of shoes with spike

Understanding Pressure

by admin

In SPM, you need to know

The definition of pressure
The formula of pressure (you need this formula to do lot of calculation.)
The SI unit of pressure
Factors affecting the magnitude of pressure

Pressure

Pressure is defined as the force acting normally per unit area. (Here, the word “normally” means perpendicularly.)

Example

As shown in the diagram above, a 20N force acts on a 4cm² surface. The force is shared equally by the surface, hence each 1 cm² of the surface withstand a force of 5N (20N/4).

The force (5N) acts on 1 unit area (1cm²) is said to be the pressure acting on the surface. Therefore, the pressure acting on the surface is 5N/cm².

Mathematically,

Unit of Pressure

The SI unit of pressure is Pascal (Pa). 1 Pa is equal to1 newton per metre2 (N/m²).

1 N/m² = 1 Pa

Factors Affecting the Magnitude of Pressure

Factors that affect the pressure acting on a surface.

Magnitude of the force.
The larger the force, the higher the pressure.
Contact area.
The larger the contact area, the lower the pressure.

Finding the force acting on a surface when the pressure and surface area are given.

Example:

A force F is acting on a surface of area 20cm², produces a pressure 2500Pa on the surface. Find the magnitude of the force.

Answer:
This is a pretty direct question. We just need to write the formula and then substitute all the related value that we have into the formula and then solve it.

However, we need to be careful about the unit. If the pressure is in Pa, then the unit of area must be in m².

1 m² = 10000 cm²

From the question,
A = 20 cm² = 0.002 m²
P = 2500 Pa

Example:
A block of wood 3 m long, 5 m wide and 1 m thick is placed on a table. If the density of the wood is 900 kgm^-3, find

the lowest pressure
the highest pressure

on the table due to the block.

Answer:
a.
Step 1: Finding the weight of the block
The volume of the block = 3 x 5 x 1 = 15m³.

Mass = Density x Volume

Mass of the block, m = (900)(15)= 13500 kg

Weight of the block = mg = 13500 x 10 = 135,000N

Step 2: Determine the surface area
The pressure exerted on a surface is inversely proportional to the area of the surface. The bigger the surface, the lower the pressure.

For the wooden block, the biggest surface, A = 5 x 3 = 15m²

Step 3: Finding pressure

b.
The pressure is the highest when the surface area is the smallest.

The smallest surface area of the block = 1 x 3 = 3m²

The highest pressure,

Example:
Two cubes made of the same material; one has sides twice as the other, lying on a table. Standing on one face, the small cube exerts a pressure M on the table. What is the pressure (in term of M) exerted by the larger cube standing on one of its faces, on the table?

Answer: