Daya dan Gerakan

Soalan Berstruktur – Memahami Tenaga

by

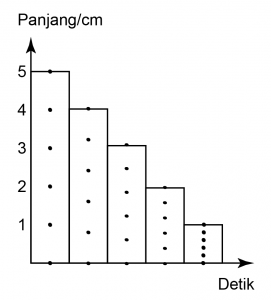
Rajah 5.1 (a) menunjukkan seorang budak lelaki imeluncur turun dari landasan kedudukan X. Rajah 5.1(b) menunjukkan graf halaju-masa budak itu dari X ke Z.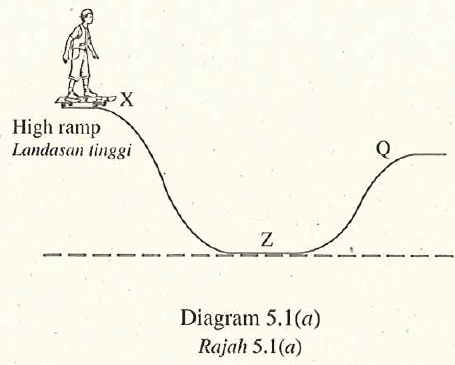

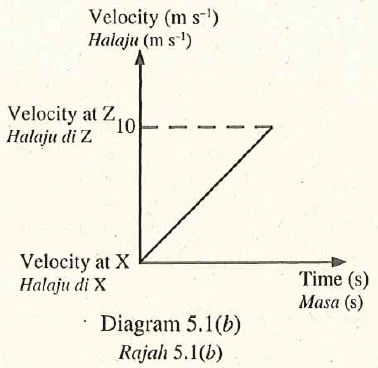
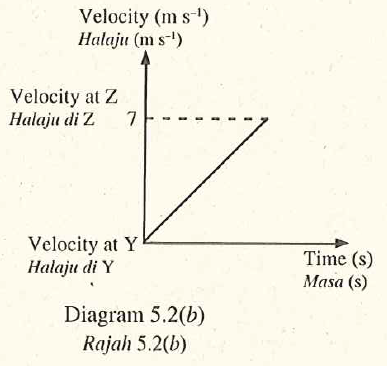
Rajah 5.2(a) menunjukkan budak lelaki yang sama meluncur turun dari kedudukan \(Y\) menggunakan landasan yang lain. Rajah \(5.2(b)\) menunjukkan graf halaju-miasa bagi budak itu dari Y ke \(Z\).

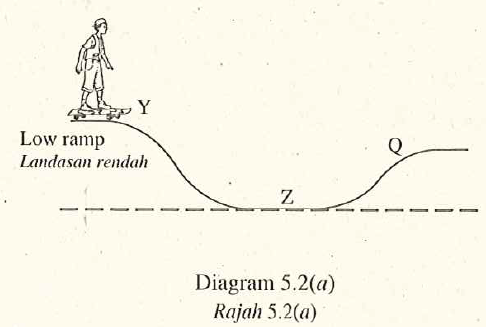
Kedua-dua landasan mempunyai kecerunan dan permukam yang sama.

  1. Namakan kuantiti fizik yang mewakili kecerunan graf halaju-masa itu. [1 markah]
    Pecutan 
  2. Perhatikan Rajah 5.1(a) dan Rajah \(5.2(a)\).
    1. Bandingkan tenaga keupayaan graviti budak itu pada \(X\) dan \(Y\).  [1 markah]

      Tenaga keupayaan graviti dalam Rajah \(5.1\) lebih besar daripada tenaga keupayaan graviti dalam Rajah \(5.2\).       
    2. Bandingkan halaju budak itu pada \(Z\) dalam kedua-dua situasi ini. [1 markah]

      Halaju budak itu di Z lebih besar daripada halajunya dalam Rajah \(5.2\).       
    3. Bandingkan tenaga kinetik budak itu pada Z dalam kedua-dua situasi ini. [1 markah] 

      Tenaga kinetik budak itu di Z lebih besar daripada tenaga kinetiknya dalam Rajah 5.2.       
  1. Berdasarkan jawapan dalam \(5 (b)\),
    1. nyatakan hubungan antara tenaga keupayaan dengan tenaga kinetik bagi budak itu. [1 markah]

      Apabila tenaga keupayaan graviti bertambah, tenaga kinetik bertambah.       
    2. nyatakan konsep fizik yang terlibat. [1 markah]
      Prinsip keabadian tenaga 
  2. Berdasarkan Rajah \(5.1\) (a),
    1. apakah yang berlaku kepada halaju budak itu apabila dia meluncur dari Z ke Q? [1 markah]
      Berkurang
    2. Berikan satu sebab kepada jawapan di \(5 (d)( i )\). [1 markah]
      Tenaga kinetik budak itu bertukar kepada tenaga keupayaan. 

Daya Dalam Keseimbangan

by

Vektor-vektor Dalam Keseimbangan


When 3 vectors are in equilibrium, the resultant vector = 0. After joining all the vectors tail to head, the head of the last vector will join to the tail of the first vector.
Apabila 3 vektor dalam keseimbangan, vektor paduannya = 0. Apabila melukis gambarajah vektor dengan  mengabungkan ekor satu vektor kepada kepala vektor yang lain, satu segitiga akan terbentuk.

Daya-daya Dalam Keseimbangan

Daya-daya dalam keseimbangan bermakna daya paduan dalam semua arah adalah sifar.
Jika daya-daya yang dikenakan ke atas satu objek adalah seimbang, mereka menghapuskan antara satu sama lain. Oleh itu, daya bersihnya ialah sifar.


Kesan :
  • Objek pegun tetap pegun [halaju = 0]
  • Objek bergerak akan terus bergerak dengan halaju malar [ pecutan = 0]

Contoh:

Rajah di atas menunjukkan satu beban berjisim 500g digantung oleh benang C. Benang C pula diikat kepada 2 benang A dan B. Cari tegangan benang A.

Jawapan:

Tegangan benang C, TC = berat beban = 5N.
Semua daya adalah dalam keseimbangan, maka,

Komponen menegak tegangan A = TC
TAcos60o = TC
TA = TC/cos60o
TA = 5/cos60o = 10N


External Link


Interactive Animation
Newton’s third Law of Motion – Java Applet

Leraian Daya

by

Leraian Vektor

  1. Satu vektor boleh dileraikan kepada dua komponen yang arahnya berserenjang antara satu sama lain.
  2. Biasanya dua komponen ini ialah
    1. komponen mengufuk
    2. komponen menegak
  3. Sama seperti kaedah segi empat selari vektor, kedua-dua komponen ini boleh digambarkan dalam gambar rajah leraian vektor seperti ditunjukkan di bawah.

Contoh:

Rajah di atas menunjukkan sebuah lori sedang menarik sebatang kayu balak dengan kabel besi. Jika tegangan pada kebel ialah 3000N dan daya geseran di antara kayu balak dan lantai ialah 500N, cari daya mengufuk yang dikenakan ke atas kayu balak itu.

Jawapan:
Komponen mengufuk daya tegangan pada kabel = 3000 cos30° =2598N
Geseran = 500N

Paduan daya mengufuk = 2598N – 500N =2098N

Contoh:

Rajah di atas menunjukkan dua daya bermagnitud 25N dikenakan ke atas satu objek berjisim 2kg. Cari pecutan objek itu dalam unit ms-2.

Jawapan:
Komponen mengufuk kedua-dua daya = 25cos45° + 25cos45° = 35.36N

Komponen menegak kedua-dua daya = 25sin45° – 25sin45° = 0N

Oleh itu, daya bersih yang dikenkan ke atas obejk itu = 35.36N

Pecutan objek boleh ditentukan daripada persamaan

F = ma
(35.36) = (2)a
a = 17.68 ms-2

External Link

Interactive Animation

Daya Paduan

by
  1. Paduan vektor ialah gabungan dua atau lebih vektor menjadi vektor tunggal yang boleh menggantikan vektor asal dan memberi kesan yang sama.
  2. Simbol untuk vektor paduan biasanya diwakili dengan dua anak panah yang sama dan sehala seperti yang ditunjukkan dalam Rajah di bawah.
  3. Penambahan dan penolakan. vektor tidak boleh dihitungkan seperti yang dilakukan. bagi kuantiti skalar
  4. Ini adalah kerana vektor ialah kuantiti yang mempunyai arah manakala kuantiti skalar tiada.

Paduan Vektor – Kaedah Segitiga



Untuk melakukan paduan vektor kaedah segitiga, sambungkan ekor bagi vektor yang kedua kepada kepala vektor pertama seperti ditunjukkan di dalam rajah di atas. Vektor berwarna merah ialah vektor paduan terbentuk.

Paduan Vektor – Kaedah Segiempat Selari


Untuk melakukan paduan vektor kaedah segiempat selari, sambungkan ekor bagi vektor pertama kepada ekor vektor pertama seperti ditunjukkan di dalam rajah di atas. Vektor berwarna merah ialah vektor paduan terbentuk.


Paduan Dua Vektor Berserenjang


Bagi vektor yang berserenjang, magnitud vektor boleh ditentukan dengan menggunakan teorem Pythagoras manakala arah vektor boleh ditentukan dengan menggunakan kaedah trigonometri seperti ditunjukkan di bawah:


Contoh:
Dua daya, P dan Q yang bermagnitud 10N dan 12N adalah berserenjang antara satu sama lain. Apakah magnitud daya paduan bagi kedua-dua daya itu apabila daya-daya itu dikenakan ke atas satu objek?

Jawapan:
Magnitud daya paduan
|F|= 10 2 + 12 2 =15.62N

Contoh:

Rajah di atas menunjukkan 4 daya yang bemagnitud 2N, 4N, 5N dan 8N dikenakan ke atas titik O. Semua daya ini adalah berserenjang antara satu sama lain. Berapakah magnitud daya paduan yang dikenakan ke atas titik O.

Jawapan:
Komponen mengufuk daya paduan terbentuk = 5 – 2 = 3N ke kanan
Komponen menegak daya paduan terbentuk =  8 – 4 = 4N ke bawah

Oleh itu, magnitud daya paduan bagi kedua-dua komponen ini,

|F|= 3 2 + 4 2 =5N


Kuantiti Vektor

by

Kuantiti Skalar dan Kuantiti Vektor

  1. Semua kuantiti fizik boleh dibahagi kepada dua jenis, iaitu
    1. Kuantiti Skalar
    2. Kuantiti Vektor
  2. Kuantiti skalar ialah kuantiti yang mempunyai magnitud sahaja seperti panjang, jarak, jisim, laju, kerja, dan sebagainya.
  3. Kuantiti vektor ialah kuantiti yang mempunyai magnitud dan arah seperti sesaran, halaju, momentum, daya, dan sebagainya.

Gambarajah Vektor

  1. Vektor biasanya diwakili oleh satu garis yang berarah.
  2. Panjang garis itu adalah magnitud vektor dan arah anak panah pula ialah arah vektor.
  3. Magnitud untuk sesuatu vektor misalnya vektor AB ditulis sebagai $v = {s \over t}$ $v = \frac{s}{t}$

Vektor Sama

  1. Dua vektor dikatakan sama jika kedua-duanya mempunyai magnitud dan arah yang sama.
  2. Dua vektor yang sama tidak semestinya bermula dan berakhir pada titik yang sama.

Vektor Negatif

Vektor negatif ialah vektor yang bermagnitud sama tetapi bertentangan arah dengan vektor yang dirujukkan.

Menentukan Pecutan daripada Pita Detik

by

Mencari Pecutan

Pecutan suatu gerakan dapat ditentukan oleh jangka masa detik dengan menggunakan persamaan berikut:
\[{a = \frac{{v – u}}{t}}\]
a = pecutan
v = halaju akhir
u = halaju awal
t = masa

Berjaga-jaga!
t ialah masa yang diambil oleh perubahan halaju dari halaju awal ke halaju akhir.

Contoh:

Pita detik di dalam rajah di atas dihasilkan oleh sebuah kereta mainan yang bergerak di atas satu landasan condong. Jika jangka masa detik yang digunakan menghasilkan 50 titik dalam satu saat, kira pecutan kereta mainan itu.

Jawapan:
Untuk mencari pecutan, kita perlu menentukan halaju awal, halaju akhir dan masa yang diambil oleh perubahan halaju berkenaan.Halaju awal,

\[\begin{array}{l}
u = \;\frac{s}{t}\;\;\\
= \;\frac{{3cm}}{{0.02s}}\;\; = 150cm\;s{\;^{ – 1}}
\end{array}\]

v= s t = 0.5cm 0.02s =25cm s −1

Masa yang diambil oleh perubahan halaju,
t = (0.5 + 4 + 0.5) ticks = 5 ticks
t = 5 × 0.02s = 0.1s

Pecutan,

a= v−u t a= 25−150 0.1 =−1250cm s −1

Contoh:

Sebuah troli ditolak menaiki satu cerun. Rajah di atas menunjukkan carta pita detik yang menunjukkan gerakan troli itu. Dalam carta itu, setiap keratan pita detik terdiri daripada 5 detik. Jika jangka masa detik itu menghasilkan 50 titik dalam satu saat, tentukan pecutan troli itu.

Jawapan:
Untuk mencari pecutan, kita perlu menentukan halaju awal, halaju akhir dan masa yang diambil oleh perubahan halaju berkenaan.Halaju awal,

u= s t = 5cm 0.1s =50cm s −1

Halaju akhir

v= s t = 1cm 0.1s =10cm s −1

Masa yang diambil oeleh perubahan halaju,
t = (2.5 + 5 + 5 + 5 + 2.5) ticks = 20 ticks
t = 20 × 0.02s = 0.4s

Pecutan,

a= v−u t a= 10−50 0.4 =−100cm s −1

Menentukan Halaju daripada Pita Detik

by

Mencari Halaju
Halaju suatu gerakan boleh ditentukan dengan menggunakan pita detik dengan persamaan berikut:
\[v = \frac{s}{t}\]
v = halaju
s = sesaran
t = masa 

Berjaga-jaga!
t ialah masa dari titik pertama ke titik terakhir bagi jarak yang diukur.

Contoh:

Rajah di atas menunjukkan sekerat pita detik yang ditarik melalui satu jangka masa detik yang bergetar 50 kali dalam satu saat. Berapakah
a. masa yang diambil dari titik pertama ke titik terakhir dalam pita detik ini?
b. halaju purata bagi pergerakan ini?
Jawapan:
a.
Terdapat 15 detik di antara titik pertama dan titik terakhir, makaMasa yang diambil = 15 × 0.02s = 0.3s

b. Jarak yang dilalui = 15cm

\[\begin{array}{l}
v = \frac{s}{t}\\
v = \frac{{15}}{{0.3}} = 50cm{s^{ – 1}}
\end{array}\]

Ciri-ciri Penting Keselamatan Kenderaan

by

Zon Remuk

Zon remuk meningkatkan masa tindakbalas perlanggaran semasa berlakunya kemalangan.
Ini menyebabkan daya impuls dikurangkan seterusnya menurunkan risiko kecederaan.

Tali Pinggang Keledar


Menghalang penumpang daripada terhumban ke hadapan atau keluar ke kenderaan apabila kenderaan dihentikan dengan mendadak.

Beg Udara Automatik


Semasa berlakunya kemalangan, beg udara mengembang dan bertindak sebagai kusyen untuk mengurangkan daya impuls jika penumpang terhumban ke hadapan.

Penyandar Kepala

Mengurangkan kederaan leher pemandu atau penumbang terhumban ke belakang apabila kereta dilanggar dari belakang.

Cermin Anti Pecah dan Berselerak

Cermin anti pecah dan berselerak digunakan sebagai cermin depan kenderaan supaya ia tidak pecah kepada serpihan kecil jika berlakunnya kemalangan. Ini mengurangkan kecederaan yang disebabkan oleh serpihan kaca yang berselerak.

Dashboard Beralas Bahan Lembut

Dashboard ditutupi dengan bahan lembut. Ini dapat memanjangkan masa tindakbalas dan seterusnya mengurangkan daya impuls apabila penumpang terhentak ke atasanya.

Collapsible Steering Columns

The steering will swing away from driver’s chest during collision. This may reduce the impulsive force acting on the driver.

Sistem Mencegah Brek Terkunci (ABS)

Mengelakkan keperluan mengepam brek apabila hendak berhenti dengan tiba-tiba dan seretusnya mencegah
roda dari terkunci dan kereta tergelongsor.

Bumper

Diperbuat daripada bahan kenyal supaya ia boleh menyerap hentakan yang kecil apabila berlakunya perlanggaran.

Ruang Keselamatan Penumpang

Badan kereta dibuat daripada keluli yang kuat dan tidak medah remuk.
Ini dapat mengelakkan penumpang daripada terkena daya dari luar secara terus.

Kesan Masa Ke Atas Magnitud Daya Impuls

by

Contoh-contoh yang melibatkan daya impuls

  1. Lompat jauh
  2. Lompat tinggi
  3. Bermain bola sepak
  4. bermain badminton
  5. bermain bola tenis
  6. bermain golf
  7. bermain besbol

Lompat Jauh

  1. Tambak lompat jauh diisi dengan pasir. Ini adalah untuk memanjangkan masa tindak balas dan seterusnya mengurangkan daya impuls yang dikenakan ke atas kaki atlit apabila mereka mendarat di atasnya.

Lompat Tinggi


(This image is licenced under the GNU Free Document Licence. The original file is from the Wikipedia.org.)

  1. Dalam acara lompat tinggi, peserta-peserta akan jatuk ke atas satu tilam yang tebal dan lembut selepas lompatan.
  2. Ini adalah untuk meningkatkan masa tindak balas dan seterusnya mengurangkan daya impuls yang dikenakan ke atas badan para peserta untuk mengelakan kecederaan.

    Melompat dan Mendarat Dari Tempat Tinggi

    1. Seseorang akan membengkkokkan kakinya semasa mendarat apabila melompat dari tempat tinggi.
    2. Ini adalah untuk memanjangkan masa tindak balas dan seterusmnya mengurangkan hentakan daya impuls yang dikenkan ke atas kaki pelompat.

    Impuls dan Daya Impuls

    by

    Impuls

    1. Hasil darab daya F dengan masa tindakannya t dikenali sebagai impuls suatu daya.
      Impuls = Ft
    2. Impuls yang dikenakan ke atas suatu objek adalah sama dengan perubahan momentum objek itu.
      Impuls = perubahan momentum = mv – mu
    3. Impuls ialah kuantitik vektor.

    Contoh:
    Sebiji bola besi berjisim 0.4kg berada dalam keadaan pegun di atas meja yang licin. Bola itu kemudian diberi satu impuls sebanyak 5.0 Ns secara mendatar. Berapakah halaju bola itu selepas tindakan itu?

    Jawapan:
    Impuls = mv – mu
    (5.0) = (0.4)v – (0.4)(0)
    0.4v = 0.5
    v = 1.25 m/s

    Halaju bola selepas tindakan = 1.25 m/s

    Daya Impuls

    1. Daya impuls ditakrifkan sebagai kadar perubahan momentum terhadap masa tindakan yang singkat bagi suatu objek yang bergerak. Secara matematik, ini ditulis sebagai
    2. Ia adalah daya yang dikenakan ke atas suatu objek dalam jangka masa yang singkat semasa perlanggaran atau letupan.

    Contoh:
    Sebuah kereta berjisim 1000kg bergerak dengan halaju 25 m/s. Kereta itu melanggar  tiang lampu jalan dan berhenti dalam masa 0.05 saat. Berapakah daya impuls yang dikenakan ke atas kereta itu dalam perlanggaran ini.

    Jawapan:
    m = 1000kg
    u = 24 m/s
    v = 0
    t = 0.05s


    Kesan Tindakan Impuls/ Daya Impuls

    1. Daya yang dikenakan ke atas suatu objek menentukan pecutan objek itu. Semakin besar daya itu, semakin tinggi pecutan objek itu.
    2. Impuls yang dikenkan ke atas suatu objek pula menentukan perubahan halaju objek itu. Semakin besar impuls yang dikenakan, semakin besar perubahan halaju objek yang dialami oleh objek itu.