Force and Motion

Structure Questions – Understanding Energy

by
Diagram 5.1 (a) shows a boy skating down a ramp from position \(X\). Diagram 5.1 \((b)\) shows the velocity-time graph of the boy from \(X\) to \(Z\).
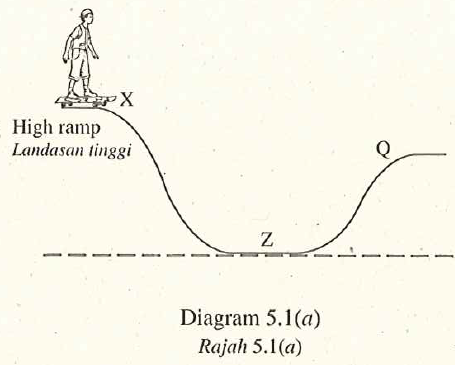
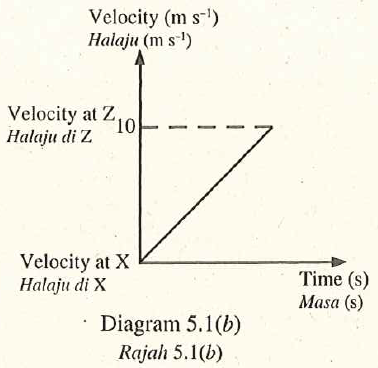
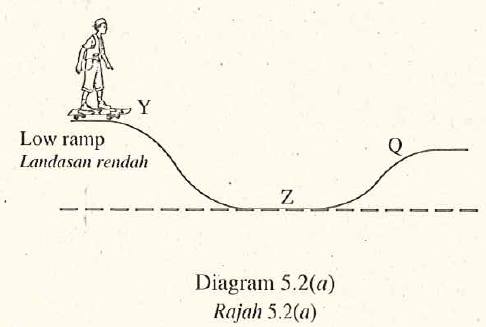
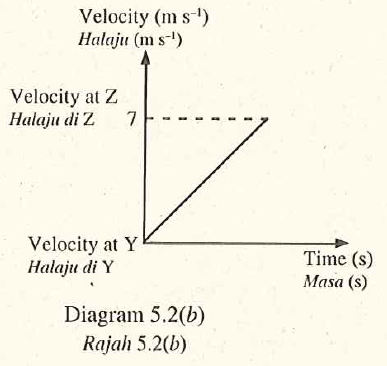
Diagram \(5.2(a)\) shows the same boy skating down from position \(Y\) by using another ramp. Diagram \(5.2(b)\) shows the velocity-time graph of the boy from \(Y\) to \(Z\).

Both ramps are of the same slope and surface.

  1. Name the physical quantity represented by the gradient of the velocity-time graph. [1 mark]
    Acceleration 
  2. Observe Diagram 5.1 (a) and Diagram \(5.2(a)\).
    1. Compare the gravitational potential energy of the boy at \(X\) and \(Y\). [1 mark]
      The gravitational potential energy in Diagram \(5.1\) is higher than that of in Diagram 5.2.
    2. Compare the velocity of the boy at \(Z\) in these two situations. [1 mark]
      The velocity of the boy at \(Z\) in Diagram \(5.1\) is higher than his velocity in Diagram 5.2.
    3. Compare the kinetic energy of the boy at \(Z\) in these two situations. [1 mark]
      The kinetic energy of the boy at \(Z\) is higher than his kinetic energy in Diagram \(5.2\).
  1. Based on the answer in \(5 (b)\),
    1. state the relationship between the gravitational potential energy and kinetic energy of the boy. [1 mark]
      When gravitational potential energy increases, the kinetic energy increases.
    2. state the physic concept involved. [1 mark]
      Principle of conseryationi of energy
  2. Based on Diagram \(5.1(a)\),
    1. what happens to the velocity of the boy when he skates from \(Z\) to \(Q\) ? [1 mark]
      Decreases
    2. Give one reason for the answer in \(5 (d)( i )\). [1 mark] 
      The kinetic energy of the boy changes to potential energy.

Kinetic Energy

by

Kinetic Energy
Kinetic energy is the energy of motion.

Equation of Kinetic Energy

Example
Determine the kinetic energy of a 2000-kg bus that is moving with a speed of 35.0 m/s.

Answer:

Kinetic Energy,

Gravity

by

Gravitational Field

A gravitational field as a region in which an object experiences a force due to gravitational attraction.

Gravitational Field Strength

  1. The gravitational field strength at a point in the gravitational field is the gravitational force acting on a mass of 1 kg placed at that point.
  2. The unit of gravitational field strength is N/kg.
  3. The gravitational field strength is denoted by the symbol “g”. g= F m g = Gravitational Field Strength
    F = Force acted on an object
    m = mass of the object.

Gravitational Acceleration

  1. The gravitational acceleration is the acceleration of an object due to the pull of the gravitational force.
  2. The unit of gravitational acceleration is ms-2
  3. Gravitational acceleratio is also denoted by the symbol “g”.

Important notes:

  1. Gravitational acceleration does not depend on the mass of the moving object.
  2. The magnitude of gravitational acceleration is taken to be 10ms-2.

    Gravitational Field Strength vs. Gravitational Acceleration

    1. Both the gravitational field strength and gravitational acceleration have the symbol, g and the same value (10ms-2) on the surface of the earth.
    2. When considering a body falling freely, the g is the gravitational acceleration.
    3. When considering objects at rest, g is the Earth’s gravitational field strength acting on it.

    Weight

    1. The weight of an object is defined as the gravitational force acting on the object.
    2. The SI unit of weight is Newton (N)

    Differences between Weight and Mass

    Weight Mass
    Depends on the gravitational field strength Independent from the gravitational field strength
    Vector quantity Scalar Quantity
    Unit Newton (N) Unit: Kilogram (kg)

    Efficiency

    by
    Efficiency

    The efficiency of a device is defined as the percentage of the energy input that is transformed into useful energy.

    Example:
    In the example above, the input power is 100J/s, the desire output power (useful energy) is only 75J/s, the remaining power is lost as undisire output. Therefore, the efficiency of this machine is

    Efficiency= 75 100 ×100%=75%

    Air Conditioner


    1. Switch off the air conditioner when not in use.
    2. Buy the air conditioner with suitable capacity according to the room size.
    3. Close all the doors and windows of the room to avoid the cool air in the room from flowing out.

    Refrigerator


    1. Always remember to close the door of refrigerator.
    2. Open the refrigerator only when necessarily.
    3. Always keep the cooling coil clean.
    4. Defrost the refrigerator regularly.
    5. Choose the refrigerator with capacity suitable for the family size.
    6. Refrigerator of large capacity is more efficient compare with refirgerator of small capacity.

    Lamp or Light Bulb


    1. Use fluorecent bulb rather than incandescent bulb. Fluorescent bulbs are much more efficient than incandescent bulbs.
    2. Use a lamp with reflector so that more light is directed towards thr desirable place.

    Washing Machine


    1. Use front-loading washing machine rather than top-loading wahing machine because it uses less water and electricity.
    2. Use washing machine only when you have sufficient clothes to be washed. Try to avoid washing small amount of clothes.

    Power

    by

    Power

    Power is the rate at which work is done, which means how fast a work is done.

    Formula:

    Example:
    An electric motor takes 20 s to lift a box of mass 20kg to a height of 1.5 m. Find the amount of work done by the machine and hence find the power of the electric motor.

    Answer:
    Work done,
    W = mgh
    W = (20)(10)(1.5) = 300J

    Power,

    Relationship between Energy and Work Done

    by

    During a conversing of energy,

    Amount of Work Done = Amount of Energy Converted

    Example:
    A trolley of 5 kg mass moving against friction of 5 N. Its velocity at A is 4ms-1 and it stops at B after t seconds. What is the work done to overcome friction?

    Answer:
    In this case, kinetic energy is converted into heat energy due to the friction. The work done to overcome the friction is equal to the amount of kinetic energy converted into heat energy, hence

    Potential Energy

    by

    Energy

    1. Energy is defined as the capacity to do work.
    2. Work is done when energy is converted from one form to another.
    3. The unit of work is Nm or Joule(J)

     

    Gravitational Potential Energy

    Gravitational potential energy is the energy stored in an object as the result of its vertical position (i.e., height).

    Formula:

     

    Example:
    A ball of 1kg mass is droppped from a height of 4m. What is the maximum kinetic energy possessed by the ball before it reached the ground?

    Answer:
    According to the principle of conservation of energy, the amount of potential energy losses is equal to the amount of kinetic energy gain.

    Maximum kinetic energy
    = Maximum potentila energy losses
    = mgh = (1)(10)(4) = 40J

     

    Elastic Potential Energy
    Elastic potential energy is the energy stored in elastic materials as the result of their stretching or compressing.

    Formula:

    Example:

    The diagram above shows a spring with a load of mass 0.5kg. The extension of the spring is 6cm, find the energy stored in the spring.

    Answer:
    The energy stored in the spring is the elastic potential energy.

     

    Finding Work Done from a Graph

    by

    Finding Work from Force-Displacement Graph
    In a Force-Displacement graph, work done is equal to the area in between the graph and the horizontal axis.

    Example:

    The graph above shows the force acting on a trolley of 5 kg mass over a distance of 10 m. Find the work done by the force to move the trolley.

    Answer:
    In a Force-Displacement graph, work done is equal to the area below the graph. Therefore, work done
    W= 1 2 (10)(8)
    W = 40Nm
    W = 40J 

    Work Done by/Against the Gravity

    by

    Work Done Against the Force of Gravity

    Example:
    Ranjit runs up a staircase of 35 steps. Each step is 15cm in height. Given that Ranjit’s mass is 45kg, find the work done by Ranjit to reach the top of the staircase.

    Answer:
    In this case, Ranjit does work to overcome the gravity.

    Ranjit’s mass = 45kg
    Vertical height of the motion, h = 35 × 0.15
    Gravitational field strength, g = 10 ms-2

    Work done, W = ?
    W = mgh
    W = (45)(10)(35 × 0.15)
    W = 2362.5J

    Work

    by

    Work

    1. Work done by a constant force is given by the product of the force and the distance moved in the direction of the force.
    2. The unit of Nm(Newton metre) or J(Joule).
    3. Work is a scalar quantity.

    Formula


    When the direction of force and motion are same, θ = 0o, therefore cosθ = 1
    Work done,

    W = F × s

    Example:

    A force of 50 N acts on the block at the angle shown in the diagram. The block moves a horizontal distance of 3.0 m. Calculate the work being done by the force.

    Answer
    Work done,
    W = F × s × cos θ
    W = 50 × 3.0 × cos30o = 129.9J

    Example:

    The diagram above shows a 10N force is pulling a metal. The friction between the block and the floor is 5N. If the distance travelled by the metal block is 2m, find

    1. the work done by the pulling force
    2. the work done by the frictional force

    Answer:
    (a) The force is in the same direction as the motion. Work done by the pulling force,
    W = F × s
    W = (10)(2) = 20J

    (b) The force is not in the same direction of motion, work done by the frictional force
    W = F × s × cos180o
    W = (5)(2)(-1) = -10J