admin

Applikasi-aplikasi Prinsip Keabadian Momentum

by

Roket

  1. Bahan api campuran hydrogen dan oksigen dibakar di dalam kebuk pembakaran.
  2. Gas ekzos dipaksa keluar dengan halaju yang amat tinggi.
  3. Gas ekzos berhalaju tinggi ini menghasilkan momentum tinggi ke belakang.
  4. Pada masa yang sama, satu momentum yang sama magnitud, tetapi ke arah depan dihasilkan ke atas roket, menyebabkan roke bergerak ke hadapan.

Enjin Jet

  1. Udara disedut masuk dari hadapan enjin. Udara itu kemudian dimampatkan oleh kompresor.
  2. Udara termampat bercampur dengan bahan api dan disalurkan ke dalam kebuk pembakaran untuk dibakar.
  3. Gas ekzos yang dihasilkan dipancut keluar dengan halaju yang tinggi melalui enjin dan memutarkan sayap turbin. Turbin itu kemudian memutarkan kompresor.
  4. Gas ekzos berhalaju tinggi disingkir keluar melalui bahagian belakang jet menghasilkan momentum yang tinggi ke arah belakang.
  5. Process ini menghasilkan satu momentum yang tinggi ke hadapan dan menolak kapal terbang jet bergerak ke hadapan. 

Recommended Videos

How A Jet Engine Works

How a jet engine works

Letupan

by

Letupan

Sebelum letupan, kedua-dua objek dalam keadaan pegun dan melekat bersama.Selepas perlanggaran, kedua-dua objek bergerak dalam arah yang bertentangan.
Jumlah momentum sebelum perlanggaran = 0.

Jumlah momentum selepas perlanggaran:

m1v1 + m2v2

Daripada Prinsip Keabadian Momentum

Jumlah Momentum Sebelum Perlanggaran = Jumlah Momentum Selepas Perlanggaran

0 = m1v1 + m2v2

m1v1 = – m2v2

(tanda negatif menunjukkan objek bergerak dalam arah bertentangan.

Contoh:
Seorang lelaki melepaskan satu tembakan daripada satu senapang yang berjisim 2.5kg. Jika jisim peluru ialah 50g dan ia bergerak dengan halaju 250 m/s selepas tembakan itu. Cari halaju senapang itu tersentak selepas tembakan.

Jawapan:
Soalan ini ialah soalan tipikal bagi kes letupan

m1 = 2.5 kg
m2 = 0.01 kg
u1 = 0 ms-1
u2 = 0 ms-1
v1 = ?
v2 = 250 ms-1

Prinsip Keabadian Momentum
0 = m1v1 + m2v2
0 = (2.5)v1 + (0.01)(250)
(2.5)v1 = -2.5v1 = -1 ms-1

External Link

Perlangaran

by
  1. Terdapat 2 jenis perlanggaran
    1. Perlanggaran kenyal.
    2. Perlanggaran tak kenyal
  2. Dalam perlanggaran kenyal, tenaga KINETIK diabadikan.
  3. Dalam perlanggaran tak kenyal, tenaga KINETIK tidak diabadikan.

Perlanggaran Kenyal

Perlanggaran kenyal ialah pelanggaran di mana jumlah tenaga kinetik dikekalkan selepas perlanggaran.

Jumlah tenaga kinetik sebelum perlanggaran
= Jumlah tenaga kinetik selepas penrlanggaran

Nota tambahan:

  • Dalam perlanggaran kenyal, kedua-dua objek terpisah sejurus selepas perlanggaran
  • Jumlah momentum diabadikan selepas perlanggaran
  • Jumlan tenaga diabadikan selepas perlanggaran
  • Jumlah tenaga KINETIK juga terabadi selepas perlanggaran.

Perlanggaran Tak Kenyal

Perlanggaran tak kenyal ialah pelanggaran di mana jumlah tenaga kinetik TIDAK dikekalkan selepas perlanggaran.


Nota tambahan:

  • Dalam perlanggaran tak kenyal, kedua-dua objek melekat (baik sementara atau kekal) sejurus selepas perlanggaran
  • Jumlah momentum diabadikan selepas perlanggaran
  • Jumlan tenaga juga diabadikan selepas perlanggaran

Contoh – Perlanggaran Tak Kenyal Sempurna
Sebuah lori bergerak berjisim 8000kg bergerak dengan halaju 30 ms-1. Lori itu kemuduan terlanggar sebuah kereta berjisim 1500kg yang bergerak dengan halaju 20 ms-1 dalam arah yang sama. Selepas perlanggaran, kedua kenderaan melekat bersama dan bergerak dengan halaju v. Cari manitud halaju, v.

Jawapan:
(PENTING: Apabila 2 objek melekat, mereka bergerak dengan halaju yang sama.)

m1 = 8000kg
m2 = 1500kg
u1 = 30 ms-1
u2 = 20 ms-1
v1 = v
v2 = v

Menurut prinsip keabadian  momentum,

m1u1 + m2u2 = m1v1 + m2v2
(8,000)(30) + (1,500)(20) = (8,000)v+ (1,500)v
270,000 = 9500v
v = 28.42 ms-1

Prinsip Keabadian Momentum

by

Prinsip Keabadian Momentum

Prinsip Keabadian Momentum menyatakan bahawa jumlah momentum sebelum perlanggaran adalah sama dengan jumlah momentum selepas perlanggaran. Jumlah momentum sebelum tindak balas = Jumlah momentum selepas tindak balas

Formula

m1u1 + m2u2 = m1v1 + m2v2
m1 = jisim jasad pertama m2 = jisim jasad kedua
u1 =  halaju awal jasad pertama
u2  = halaju awal jasad kedua v1 =  halaju akhir jasad pertama v2 =  halaju akhir jasad kedua
Contoh – Kedua-dua objek bergerak dalam arah yang sama sebelum perlanggaran Sebuah kereta berjjisim 600kg bergerak dengan halaju 60km/j. Ia kemudian berlanggar dengan kereta B yang berjisim 800kg dan bergerak dengan halaju 20 ms-1 dalam arah yang sama. Jika kereta B bergerak dengan halaju 30 ms-1 akibar daripada hentakan itu, berapakah halaju kereta A sejurus selepas perlanggaran itu?Jawapan: m1 = 600kg m2 = 800kg u1 = 40 ms-1 u2 = 20 ms-1 v1 = ? v2 = 30 ms-1 Prinsip Keabadian Momentum m1u1 + m2u2 = m1v1 + m2v2 (600)(40) + (800)(20) = (600)v1 + (800)(30) 40000 = 600v1 + 24000 600v1 = 16000 v1 = 26.67 ms-1
Contoh – Kedua-dua objek bergerak dalam arah yang berlawanan sebelum perlanggaran Sebiji bola 0.50kg bergerak dengan 6.0 ms-1 berlanggar dengan satu lagi bola 1.0kg yang bergerak dengan laju 12.0 ms-1 dalam arah yang berlawanan. Bola 0.50kg itu berundur ke belakang dengan laju 14.0 ms-1 selepas perlanggaran. Cari halaju bola yang kedua selepas perlanggaran.Jawapan: m1 = 0.5 kg m2 = 1.0 kg u1 = 6.0 ms-1 u2 = -12.0 ms-1 v1 = -14.0 ms-1 v2 = ? (PENTING: halaju adalah negatif apabila suatu objek bergerak dalam arah berlawanan) Prinsip keabadian momentum, m1u1 + m2u2 = m1v1 + m2v2 (0.5)(6) + (1.0)(-12) = (0.5)(-14) + (1.0)v2 -9 = – 7 + 1v2 v2 = -2 ms-1

Momentum

by

Momentum

  1. Momentum ditakrifkan sebagai hasil darab jisim dan halaju.
  2. Momentum ialah satu kuantiti vektor. Ia mempunyai magnitud dan arah.
  3. Unit S.I. bagi momentum ialah kgms-1

Formula:


Contoh:
Seorang pelajar melepas sebiji bola berjisim 2kg dari ketinggian 5m. Berapakah momentum bola itu sejurus sebelum terhempas ke atas lantai?

Jawapan:
Untuk mencari momentum, kita perlu tahu jisim dan halaju bola itu sejurus sebelum ia terhempas di atas lantai.

Diberi bahawa jisim bola, m = 2kg.

Halaju bola tidak diberi secara langsung. Bagaimanapun, kita boleh menentukan halaju bola dengan menggunakan persamaan gerakan dengan pecutan seragam.

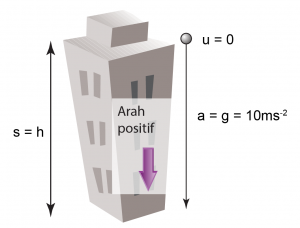
Ini ialah gerakan jatuh bebas,
Halaju awal, u = 0
Pecutan, a = pecutan graviti, g = 10ms-2
Sesran, s = ketinggian = 50m.
Halaju akhir = ?

Dengan menggunakan persamaan
v2 = u2 + 2as
v2 = (0)2 + 2(10)(5)
v = 10ms-1

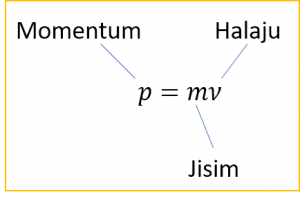
Momentum bola
p = mv =(2)(10) = 20 kgms-1

Hukum Gerakan Newton Pertama

by

Hukum

Hukum Newton Pertama menyatakan bahawa
Suatu objek dalam keadaan pegun akan terus berada dalam keadaan pegun, atau jika bergerak akan terus bergerak dengan halaju tetap pada suatu garis lurus, kecuali dikenakan suatu daya luar.
Hukum Newton Pertama adalah sejajar dengan konsep inersia, di masa suatu jirim cenderung mengekalkan keadaan pergerakannya.

Inersia

by

Jisim

  1. Jisim ditakrifkan sebagai kuantiti jirim.
  2. Unit S.I. bagi jisim ialah kilogram (kg)
  3. Jisim ialah kuantiti skalar.

Inersia

Inersia suatu objek ialah sifat semula jadinya yang menentang sebarang perubahan keadaan asalnya, sama ada keadaan rehat atau keadaan gerakan.

Situasi Tentang Inersia

Keadaan Asal Objek yang Pegun

Situasi 1

Apabila kadbod disentap dengan cepat, duit syiling jatuh terus ke dalam gelas.

Penerangan:

  • Inersia duit syiling menentang usaha untuk menggerakannya ke tepi dan mengekalkan keadaan pegunnya.
  • Oleh itu, duit syiling tidak bergerak bersama kadbod tetapi jatuh ke dalam gelas selepas kadbod dialihkan.


    Situasi 2

    Apabila sebuah buku disentap dari selonggok buku, buku yang lain di atasnya akan jatuh ke bawah.

    Penerangan:

    • Inersia buku-buku yang pegun di atas cuba menentang perubahan ke atas keadaan asalnya.
    • Oleh itu, apabila buku tengah disentap, buku-buku di atas tidak bergerak ke sisi tetapi jatuh ke bawah.

    Menarik Benang

    1. Benang ditarik perlahan-lahan – Benang A akan putus.

    Penerangan:

    • Tegangan pada benang A lebih tinggi daripada benang B.
    • Tegangan benang A = Berat beban + daya tarikan.
    • Tali A akan putus jika daya yang dikenakan ke atasnya melebihi had daya yang boleh ditanggung.

    2. Benang disentak – Benang B akan putus.

    Penerangan:

    • Akibat daripada kesan inersia pada beban, daya tarikan yang dikenakan tidak disampaikan kepada benang A.
    • Akibatnya, benang B terputus  jika daya yang dikenakan ke atasnya melebihi had daya yang boleh ditanggung.

    Hubungkait Antara Jisim dan Inersia

    Baldi yang penuh dengan pasir adalah lebih sukar digerakkan daripada keadaan pegun dan juga lebih sukar dihentikan daripada berayun.

    Penerangan:

    • Semakin besar jisim sesuatu objek, semakin besar kesan inersianya.
    • Akibattnya, semakin susah objek itu mengubahkan keadaan pegun atau gerakannya.


      Troli kosong lebih senang digerak dan dikawal


      1. Troli yang kosong lebih senang digerakan berbanding dengan troli yang penuh.
      2. Ini adalah kerana troli yang penuh mempunyai jisim yang lebih besar. Oleh itu, kesan inersianya juga lebih besar.
      3. Akibatnya, troili yang penuh lebih susah mengubahkan keadaan pegun atau gerakannya.

      Kesimpulan

      1. Semakin besar jisim sesuatu objek, semakin besar inersia objek itu.
      2. Jisim merupakan halangan kepada pergerakan. Semakin besar jisim sesuatu objek, semakin sukar ia digerakan.
      3. Tanpa tindakan daya paduan, suatu objek mungkin dalam 2 keaadaan gerakan.
        1. Pegun
        2. Bergerak dengan halaju malar dalam garis lurus

      Graf bagi Objek Jatuh Bebas

      by
      1. Jatuh bebas ialah satu kejatuhan yang disebabkan oleh daya tarikan graviti tanpa kesan rintangan udara dan daya luaran.
      2. Pecutan bagi gerakan jatuh bebas adalah sentiasa malar.
      3. Di permukaan bumi, pecutan ini ialah 10ms-2, dan dinamakan sebagai pecutan graviti.
      4. Dalam SPM, anda perlu mengetahui graf gerakan jatuh bebas bagi gerakan-gerakan berikut:
        1. Meloncarkan objek ke atas
        2. Melepaskan objek dari kawasan tinggi.
        3. Objek jatuh di atas lantai dan melantun.

      Melancarkan Objek ke Atas

      1. Apabila anda melancarkan satu objek ke atas, halajunya berkurang pada kadar yang tetap, maka dalam graf halaju masa ia diwakili oleh satu garis lurus dengan kecerunan negatif.
      2. Sejak halajunya berkurang dengan kadar yang tetap, maka pecutannya adalah malar.
      3. Pecutannya adalah negatif kerana lajunya berkurang dalam arah positif.
      4. Oleh itu, dalam graf pecutan-masa, gerakan ini diwakili oleh satu garis mengufuk di dalam domain negatif.

      Graf Halaju-Masa

      Graf Pecutan-Masa

          Melepaskan Objek dari Kawasan Tinggi

          1. Apabila satu objek dilepaskan dari satu kewasan tinggi, halajunya bertambah dengan kadar yang tetap.
          2. Oleh itu dalam graf halaju-masa ia diwakili oleh satu garis lurus dengan kecerunan positif.
          3. Oleh kerana halajunya bertambah dengan kadar yang malar, maka pecutannya adalah seragam.
          4. Pecutannya adalah positif kerana lajunya bertambah dan objek bergerak dalam arah positif.
          5. Oleh itu, dalam graf pecutan-masa, gerakan ini diwakili oleh satu garis mengufuk di dalam domain positif.

          Graf Halaju-Masa

          Graf Pecutan-Masa

          Objek Jatuh di atas Lantai Kemudian Melantun
          Graf Halaju-Masa

          Graf Pecutan-Masa

          Gerakan Jatuh Bebas

          by

          Gerakan Jatuh Bebas

          1. Jatuh bebas ialah satu kejatuhan objek yang disebabkan oleh daya tarikan graviti sebagai satu-satunya daya yang dikenakan ke atas objek itu.
          2. Gerakan jatuh bebas hanya berlaku di dalam vakum.

          Kes Jatuh Bebas 1 – Jatuh Dari Tempat Tinggi


          Apabila satu objek dilepaskan dari satu tempat tinggi,

          1. Halaju awalnya, u = 0.
          2. pecutannya sama dengan pecutan graviti, g, iaitu 10ms-2 in SPM.
          3. sesaran objek apabila ia memcapai lantai sama dengan ketinggian di mana objek itu dilepaskan, h.

          Kes Jatuh Bebas 2 – Melancarkan Objek ke Atas


          Jika satu objek dilancarkan ke atas secara menegak,

          1. pecutannya = -g (-10ms-2)
          2. halajunya adalah sifar apabila ia mencapai ketinggian maksimum.
          3. sesaran objek apabila mencapai ketinggian maksimum sama dengan ketinggian objek, h
          4. masa yang diambil untuk bergerak ke ketinggian maksimum sama dengan masa yang diambil untuk jatuh ke kedudukan asalnya dari ketinggian maksimum.

            Graf Halaju-Masa

            by
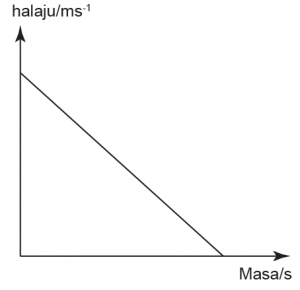
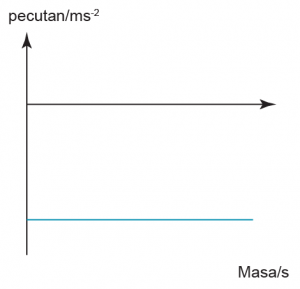
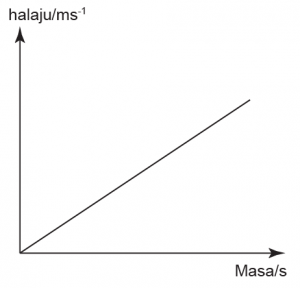
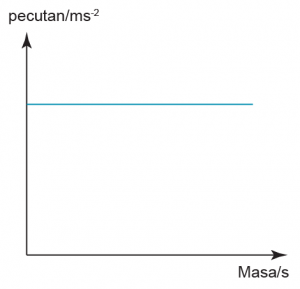
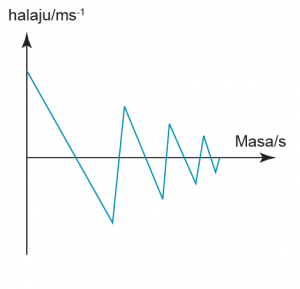
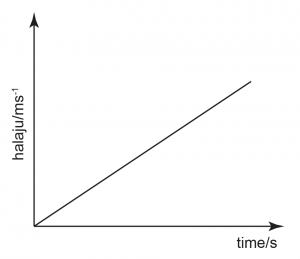
            Graf Halaju – Masa Daripada persamaan \[Pecutan\; = \;\frac{{Perubahan{\rm{ }}halaju}}{{Masa}}\] Pecutan = kecerunan dalam graf halaju melawan masa manakala Sesaran = luas dibawah graf

            Analisa Graf Halaju – Masa

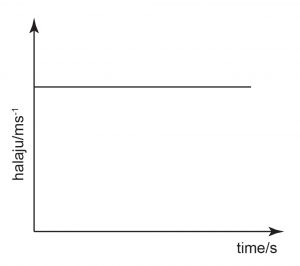            Kecerunan = 0,
            pecutan = 0 (Halaju seragam)
            Kecerunan malar,
            pecutan seragam

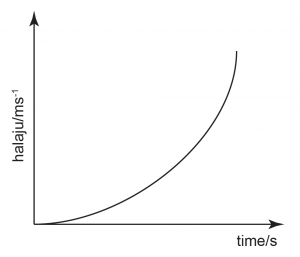            Kecerunan bertambah,
            pecutan bertambah
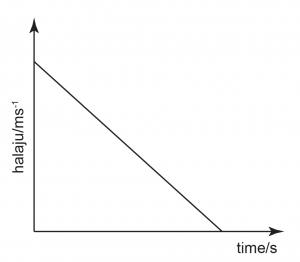            Kecerunan negatif dan malar,
            nyahpecutan seragam.
            Kecerunan = berkurang,
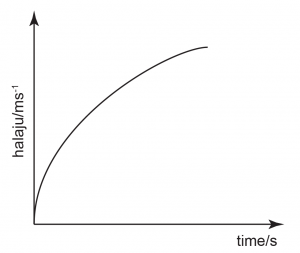            pecutan berkurang