admin

Kepekaan

by

Kepekaan

Kepekaan satu alat pengukur ialah kebolebannya mengesan perubahan yang kecil dalam kuantiti iizik yang diukur.
  1. Kepekaan satu alat pengukur ialah kebolebannya mengesan perubahan yang kecil dalam kuantiti iizik yang diukur.
  2. Satu alat pengukur adalah lebih peka jika nilai bahagian skala yang terkecilnya adalah lebih kecil.
  3. Satu pembaris meter adalah lebih peka daripada satu pita pengukur sebab nilai senggatan terkecil pembaris, 0.1 cm adalah lebih kecil daripada nilai senggatan terkecil pita pengukur, 0.5 cm.

    Recommended Videos

    Accuracy and Precision

    Accuracy and Precision

    Kejituan

    by

    Kejituan

    Kejituan pengukuran ialah betapa hampir suatu nilai pengukuran kepada nilai sebenar.
    1. Kejituan pengukuran ialah betapa hampir suatu nilai pengukuran kepada nilai sebenar.
    2. Satu ukuran adalah lebih jitu jika nilainya adalah lebih dekat dengan nilai yang sebenar.
    3. Perbezaan antara satu ukuran dengan nilai sebenar dikenal sebagai ralat.
    4. Kejituan suatu pengukuran boleh ditambah dengan
      1. menggunakan alat pengukuran yang lebih peka,
      2. mengambil beberapa bacaan ulangan,
      3. mengelakkan ralat paralaks dan ralat sifar.
    5. Maksud kepersisan dan kejituan dapat dijelaskan dengan mengkaji tembakan-tembakan yang dilakukan oleh tiga orang peserta dalam pertandingan menembak.

    Kepersisan

    by

    Kepersisan Precision

    1. Kepersisan sesuatu alat pengukur ialah kebolehan alat itu untuk memberi bacaan-bacaan yang konsisten apabila kuantiti fizik yang sama diukur lebih daripada satu kali.
    2. Ukuran bagi satu kuantiti adalah konsisten jika semuanya adalah hampir dengan satu sama lain.
    3. Satu ukuran adalah lebih persis jika sisihan relatifnya lebih kecil.
    4. Kepersisan satu ukuran boleh ditambah dengan
      1. menggunakan kanta pembesar semasa membaca skala alat pengukur. Kanta pembesar membentukkan satu imej yang,, besar, maka skala itu dapat dilihat dengan lebih jelas.
      2. Mengelakan ralat paralaks.

    Sisihan Relatif Relative Deviation

    Sisihan Relatif =  sisihan purata bacaan purata ×100%
    1. Sisihan suatu bacaan ialah perbezaan antara bacaan itu dengan nilai purata.

    Contoh:

    Bacaan-bacaan diameter
    2.14cm
    2.13cm
    2.17cm
    2.15cm
    2.16cm

    Purata diameter =  2.14+2.13+2.17+2.15+2.16 5 = 10.75 5 =2.15cm

    Bacaan Sisihan
    2.14 cm
    		 ( 2.15 – 2.14 ) cm = 0.01 cm
    2.13 cm
    		 ( 2.15 – 2.13 ) cm = 0.02 cm
    2.17 cm
    		 ( 2.17 – 2.15 ) cm = 0.02 cm
    2.15 cm
    		 ( 2.15 – 2.15 ) cm = 0 cm
    2.16 cm
    		 ( 2.16 – 2.15 ) cm = 0.01 cm

    sisihan purata =  0.01+0.02+0.02+0+0.01 5 = 0.06 5 =0.012cm
    Sisihan Relatif =  sisihan purata bacaan purata ×100% Sisihan Relatif =  0.012 2.15 ×100%=0.56%


    Pengukuran dan Ralat

    by

    Ralat Error

    1. Ralat ialah beza antara nilai sebenar bagi satu kuantiti fizik dan nilai yang didapati dalam pengukuran.
    2. Oleh kerana nilai kuantiti yang sebenar tidak diketahui, maka ralat yang sebenar juga tidak diketahui.
    3. Bagaimanapun, ralat satu ukuran biasanya dapat dianggar.
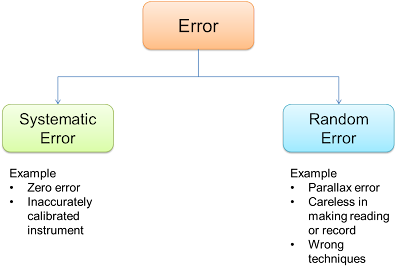
    4. Terdapat 2 jenis ralat utama
      1. Ralat bersistem 
      2. Ralat rawak

      English Notes:

      1. Error is the difference between the actual value of a quantity and the value obtained in measurement.
      2. There are 2 main types of error 
        1. Systematic Error 
        2. Random Error

      Ralat Bersistem Systematic Error

      1. Ralat bersistem ialah ralat yang cenderung untuk mengalihkan semua pengukuran secara bersistem sehingga nilai minnya tersesar daripada nilai sebenar.
      2. Ralat bersistem mengakibatkan semua bacaan yang diperoleh sama ada terlalu besar atau terlalu kecil.
      3. Ralat bersistem tidak dapat dihapuskan dengan mengambil purata terhadap beberapa bacaan yang diulang-ulang. Contoh ralat bersistem termasuk:
      4. Contoh-contoh ralat bersistem termasuk
        1. ralat sifar, iaitu bacaan bukan sifar alat pengukur apabila bacaan sebenar adalah sifar. 
        2. ketidaktepatan dalam menentukur alat-alat pengukur.
        3. masa tindak balas orang yang menjalankan eksperimen.
        4. cara mengguna alat pengukur yang tidak betul
      5. Ralat bersistem dapat dihapuskan/dikurangkan dengan cara-cara berikut.
        1. Menjalankan eksperimen dengan berhati-hati sepanjang masa. 
        2. mengulangi eksperimen dengan alat-alat pengukur yang berbeza.

      English Notes:

      1. Systematic errors are errors which tend to shift all measurements in a systematic way so their mean value is displaced. Systematic errors can be compensated if the errors are known.
      2. Examples of systematic errors are 
        1. zero error, which cause by an incorrect position of the zero point, 
        2. an incorrect calibration of the measuring instrument. 
        3. consistently improper use of equipment. 
      3. Systematic error can be reduced by 
        1. Conducting the experiment with care. 
        2. Repeating the experiment by using different instruments.

      Recommended Videos

      Systematic Error

      Systematic Error – Part 2

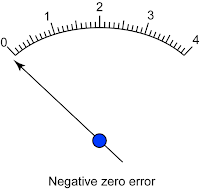
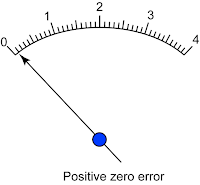
      Ralat Hujung/Ralat Sifar Zero error

      1. Ralat hujung atau ralat sifar ialah bacaan bukan sifar alat pengukur apabila bacaan sebenar adalah sifar.
      2. Contoh ralat hujung adalah
        1. Hujung pembaris meter yang haus menyebabkan skala pada tanda “0” tidak jelas. Ia boleh dielakkan dengan memulakan pengukuran dari tanda 1 cm.
        2. Bacaan jam randik yang jarumnya tidak kembali ke tanda “0” apabila tompol “reset” ditekan. Ia boleh dihapuskan dengan menolak ralat sifar daripada setiap bacaan.
        3. Bacaan meter elektrik seperti ammeter apabila tiada arus melaluinya.

      Contoh (Bacaan Ammeter apabila tiada arus mengalir melaluinya)

      (Tanpa ralat sifar: Penunjuk ammeter berada tepat di atas tanda sifar.)
      (Ralat sifar negatif: Penunjuk ammeter menunjukkan bacaan negatif walaupun tiada arus mengalir melaluinya.)
      (Ralat sifar positif: Penunjuk ammeter menunjukkan bacaan positif walaupun tiada arus mengalir melaluinya.)

      English Notes:

      1. A zero error arises when the measuring instrument does not start from exactly zero.
      2. Zero errors are consistently present in every reading of a measurement.
      3. The zero error can be positive or negative.

      Recommended Videos

      Zero Error

      Ralat Rawak Random Errors

      1. Ralat rawak adalah disebabkan perubahan keadaan yang tidak dapat diramalkan dan tidak dapat dikawal oleh pemerhati.
      2. Ia mengakibatkan satu serakan bacaan sekitar bacaan sebenar.
      3. Contoh ralat rawak ialah:
        1. ralat paralaks yang disebabkan kedudukan mata yang tidak betul apabila mengambil bacaan.
        2. mengambil bacaan-bacaan yang berubah dengan masa.
        3. silap membilang
        4. sebahagian isi padu air tertuang keluar tanpa disedari.
      4. Ralat rawak dapat dikurangkan dengan mengulangi bacaan dan kemudian mengambil purata bacaan-bacaan itu. 

      English Notes:

      1. Random errors arise from unknown and unpredictable variations in condition.
      2. It fluctuates from one measurement to the next.
      3. Random errors are caused by factors that are beyond the control of the observers.
      4. Random error can cause by
        1. personal errors such as human limitations of sight and touch. 
        2. lack of sensitivity of the instrument: the instrument fail to respond to the small change. 
        3. natural errors such as changes in temperature or wind, while the experiment is in progress. 
        4. wrong technique of measurement. 
      5. One example of random error is the parallax error. Random error can be reduced by 
        1. taking repeat readings 
        2. find the average value of the reading.

      Recommended Videos

      Random Error


      Ralat paralaks

      1. Ralat paralaks ialah kesilapan yang dilakukan semasa membaca skala alat pengukur.
      2. Bacaan skala yang diperoleh adalah salah sebab kedudukan mata relatif kepada skala yang kurang sesuai semasa membaca skala.



      English Notes:

      A parallax error is an error in reading an instrument due to the eye of the observer and pointer are not in a line perpendicular to the plane of the scale.

      Recommended Videos

      Parallax Error

      Imbuhan

      by
      1. Imbuhan ialah awalan faktor daraban yang digunakan untuk mewakili sesuatu nilai yang sangat besar atau sangat kecil.
      2. Jadual di bawah menunjukkan imbuhan yang anda perlu ketahui dalam silibus SPM.

      Penukaran Imbuhan 

      Imbuhan ke Unit SI

      Contoh 1:
      Diberi bahawa frekuensi suatu gelombang radio ialah 350M Hz. Berapah frekuensi gelombang radio itu dalam unit Hz?
      Jawapan:

      Mega (M) = 1,000,000 or 106

      Maka,
      350MHz = 350 x 106Hz

      Contoh 2:
      Diberi bahawa ketebalan sekeping filem ialah 25nm. Berapakah ketebalan filem itu dalam unit meter?
      Jawapan:

      nano (n) = 0.000000001 or 10-9

      Maka
      25nm = 25 x 10-9m

      Unit SI ke Imbuhan

      Contoh 3:
      0.255 s adalah sama dengan berapa ms.
      Jawapan:

      mili (m) = 0.001 or 10-3

      Untuk menulis sesuatu nombor bersama imbuhannya, kita membahagikan nombor itu dengan nilai imbuhan berkenaan

      0.0255 s = 0.0255 ÷ 10-3 = 25.5 ms

      Contoh 4:
      Tukarkan 265,500,000 W kepada unit GW.

      Jawapan:

      Gega (G) = 1,000,000,000 or 109

      Maka
      265,500,000 W = 265,500,000 ÷ 109 = 0.2655GW

      Pautan Luar

      The NIST Reference on Prefixes

      Bentuk Piawai dan Angka Bererti

      by

      Bentuk Piawai 

      1. Bentuk piawai ialah satu cara mudah untuk menulis nombor yang amat besar atau amat kecil.
      2. Dalam bentuk piawai, satu nombor dipisahkan kepada 2 bahagian, iaitu 
        1. satu nombor sahih dengan nilai mutlak di antara 1 dan 10 
        2. satu darjah nilai magnitud yang ditulis sebagai kuasa bagi 10.

        Recommended Videos

        Scientific Notation

        Scientific Notation – Explained!

        Angka Bererti

        1. Dalam pengukuran, bilangan angka bererti mangaitkan kepastian sesuatu pengukuran.
        2. Apabila bilangan angka bererti meningkat, kepastian terhadap pengukuran dibuat juga meningkat, bermakna kita  lebih pasti akan kejituan pengukuran yang di buat.


        Contoh:

        Laju cahaya di dalam vakum = 299 792 458 ms-1 = 3.00 x 108 ms-1 (betul kepada 3 angka bererti)

        Contoh:
        Tuliskan bilangan angka bererti (a.b.) bagi nombor-nombor berikut:

        1. 135 m, (____a.b.) 
        2. 0.013s (____a.b.) 
        3. 0.2000A (____a.b.) 
        4. 25.10 g (____a.b.) 
        5. 3700km (____a.b.) 
        6. 0.003kg (____a.b.) 
        7. 1.54 x 10-3  (____a.b.) 
        8. 0.001200 (____a.b.)

        Answer:

        1. 135 m, ( 3 a.b.) 
        2. 0.013s ( 2 a.b.) 
        3. 0.2000A ( 4 a.b.) 
        4. 25.10 g ( 4 a.b.) 
        5. 3700km ( 4 a.b.) 
        6. 0.003kg ( 1 a.b.) 
        7. 1.54 x 10-3 ( 3 a.b.) 
        8. 0.001200 ( 4 a.b.)

          Recommended Videos

          Number of Significant Figures – Exercise

          Significant Figures

          More on Significant Figures