admin

Structure Questions – Understanding Energy

by
Diagram 5.1 (a) shows a boy skating down a ramp from position \(X\). Diagram 5.1 \((b)\) shows the velocity-time graph of the boy from \(X\) to \(Z\).
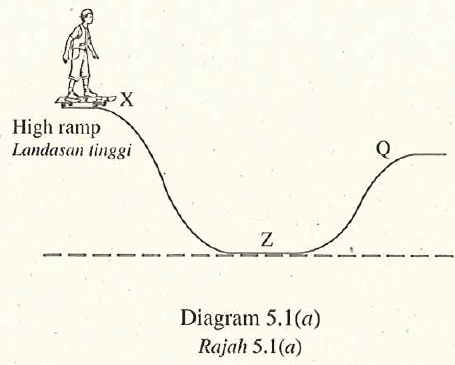
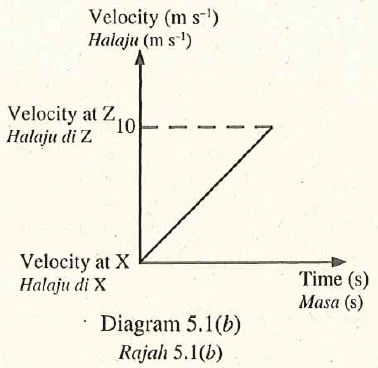
Diagram \(5.2(a)\) shows the same boy skating down from position \(Y\) by using another ramp. Diagram \(5.2(b)\) shows the velocity-time graph of the boy from \(Y\) to \(Z\).

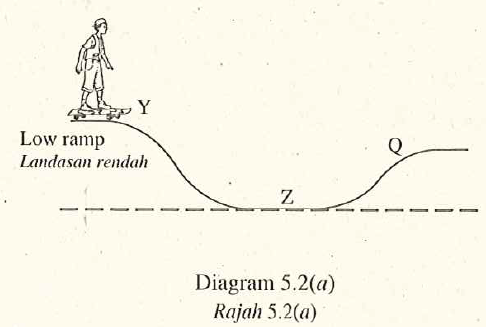
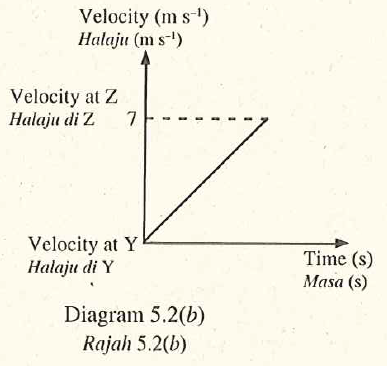
Both ramps are of the same slope and surface.

  1. Name the physical quantity represented by the gradient of the velocity-time graph. [1 mark]
    Acceleration 
  2. Observe Diagram 5.1 (a) and Diagram \(5.2(a)\).
    1. Compare the gravitational potential energy of the boy at \(X\) and \(Y\). [1 mark]
      The gravitational potential energy in Diagram \(5.1\) is higher than that of in Diagram 5.2.
    2. Compare the velocity of the boy at \(Z\) in these two situations. [1 mark]
      The velocity of the boy at \(Z\) in Diagram \(5.1\) is higher than his velocity in Diagram 5.2.
    3. Compare the kinetic energy of the boy at \(Z\) in these two situations. [1 mark]
      The kinetic energy of the boy at \(Z\) is higher than his kinetic energy in Diagram \(5.2\).
  1. Based on the answer in \(5 (b)\),
    1. state the relationship between the gravitational potential energy and kinetic energy of the boy. [1 mark]
      When gravitational potential energy increases, the kinetic energy increases.
    2. state the physic concept involved. [1 mark]
      Principle of conseryationi of energy
  2. Based on Diagram \(5.1(a)\),
    1. what happens to the velocity of the boy when he skates from \(Z\) to \(Q\) ? [1 mark]
      Decreases
    2. Give one reason for the answer in \(5 (d)( i )\). [1 mark] 
      The kinetic energy of the boy changes to potential energy.

5 Structured Questions – Cathode Ray Oscilloscope

by

Diagram \(4.1\) shows a bright spot, P, formed on the screen of a cathode-ray oscilloscope, C.R.O. when it is switched on.

  1. What is the meaning of cathode ray? [1 mark]
    High speed election beam.
  2. Explain how the bright spot is formed on the screen of the C.R.O. [2marks]
    When the electrons hit the fluorescent screen, the screen glows and forms a light spot. The kinetic energy of the electrons changes to light energy.
  3. Diagram \(4.2\) shows the bright spot is displaced to \(Q\) when a direct current, d.c. supply, is connected to the Y-input of the C.R.O.

The Y-gain of the C.R.O is set at \(2 V /\) division. Calculate the input voltage of the d.c. supply. [2 marks]

Output voltage
\[
\begin{aligned}
&=2 V +2 V \\
&=4 V
\end{aligned}
\]

  1. Diagram \(4.3\) shows an alternating current, a.c. supply, is connected to the C.R.O. The Y-gain of the C.R.O. remains at \(2 V /\) division.

Draw the output signal on the screen in Diagram \(4.3\) when the peak voltage of the a.c. supply is \(6 V\) and the time base is switched off. [2 marks]

Structured Questions – Half Life

by

Diagram 3 shows the activity-time graph of radioisotope Potassium-42. This radioisotope emits beta particles and is used as a tracer to measure the quantity of salt in human body.

  1. State one characteristic of beta particles. [1 mark]
    Negatively charged 
  2. Based on Diagram 3 , determine the half-life of Potassium-42. Show on the graph how you determine the half-life of Potassium. [2 mark]
    12 hours
  3. Based on the half life, state why Potassium-42 is suitable to be used as the tracer. [1 mark]
    Potassium-42 has short half-life, hence overexposure does not occur.
  4. Calculate the time taken for radioistope Potassium-42 to reduce \(\frac{1}{8}\) of its initial activity. [2 marks]
    \(1 \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{2} \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{4} \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{8}\)
    The time taken for the activity of the potassium- 42 becomes \(\frac{1}{8}\) of its initial activity.
    \[
    \begin{aligned}
    &=3 T _{\frac{1}{2}} \\
    &=3 \times 12 \text { hours } \\
    &=36 \text { hours } 
    \end{aligned}
    \]

Soalan Berstruktur – Memahami Tenaga

by

Rajah 5.1 (a) menunjukkan seorang budak lelaki imeluncur turun dari landasan kedudukan X. Rajah 5.1(b) menunjukkan graf halaju-masa budak itu dari X ke Z.

Rajah 5.2(a) menunjukkan budak lelaki yang sama meluncur turun dari kedudukan \(Y\) menggunakan landasan yang lain. Rajah \(5.2(b)\) menunjukkan graf halaju-miasa bagi budak itu dari Y ke \(Z\).

Kedua-dua landasan mempunyai kecerunan dan permukam yang sama.

  1. Namakan kuantiti fizik yang mewakili kecerunan graf halaju-masa itu. [1 markah]
    Pecutan 
  2. Perhatikan Rajah 5.1(a) dan Rajah \(5.2(a)\).
    1. Bandingkan tenaga keupayaan graviti budak itu pada \(X\) dan \(Y\).  [1 markah]

      Tenaga keupayaan graviti dalam Rajah \(5.1\) lebih besar daripada tenaga keupayaan graviti dalam Rajah \(5.2\).       
    2. Bandingkan halaju budak itu pada \(Z\) dalam kedua-dua situasi ini. [1 markah]

      Halaju budak itu di Z lebih besar daripada halajunya dalam Rajah \(5.2\).       
    3. Bandingkan tenaga kinetik budak itu pada Z dalam kedua-dua situasi ini. [1 markah] 

      Tenaga kinetik budak itu di Z lebih besar daripada tenaga kinetiknya dalam Rajah 5.2.       
  1. Berdasarkan jawapan dalam \(5 (b)\),
    1. nyatakan hubungan antara tenaga keupayaan dengan tenaga kinetik bagi budak itu. [1 markah]

      Apabila tenaga keupayaan graviti bertambah, tenaga kinetik bertambah.       
    2. nyatakan konsep fizik yang terlibat. [1 markah]
      Prinsip keabadian tenaga 
  2. Berdasarkan Rajah \(5.1\) (a),
    1. apakah yang berlaku kepada halaju budak itu apabila dia meluncur dari Z ke Q? [1 markah]
      Berkurang
    2. Berikan satu sebab kepada jawapan di \(5 (d)( i )\). [1 markah]
      Tenaga kinetik budak itu bertukar kepada tenaga keupayaan. 

Soalan Berstruktur – Osiloskop Sinar Katod

by

Rajah \(4.1\) menunjukkan satu tompok cerah, P, terbentuk pada skrin osiloskop sinar katod, O.S.K., apabila suis dihidupkan.

  1. Apakah maksud sinar katod? [1 markah]

    Pancaran elektron pada kelajuan tinggi. 
  2. Terangkan bagaimana tompok cerah itu terbentuk pada skrin O.S.K. itu. [2 markah ]
    Apabila elektron menghentam skrin berpendafluor; skrin itu menyala dan membentuk satu tompok cahaya. Tenaga kinetik elektron bertukar kepada tenaga cahaya.
  3. Rajah \(4.2\) menunjukkan tompok cerah itu disesarkan kepada Q apabila bekalan arus terus, a.t., disambungkan kepada input-Y bagi O.S.K. itu.

Gandaan-Y bagi O.S.K. itu dilaraskan pada \(2 V /\) bahagian. Hitung voltan input bagi bekalan a.t. itu. [2 markah]

Voltan output
\[
\begin{aligned}
&=2 V +2 V \\
&=4 V
\end{aligned}
\]

  1. Rajah \(4.3\) menunjukkan bekalan arus ulang-alik, a.u,, disambungkan kepada O.S.K. itu. Gandaan-Y bagi O.S.K. itu dikekalkan pada \(2 V /\) bahagian.

Lukis isyarat output pada skrin di Rajah \(4.3\) apabila voltan puncak bekalan a.u. ialah \(6 V\) dan dasar masa dimatikan. [2 markah]

Soalan Berstruktur – Separuh Hayat

by

Rajah 3 menunjukkan graf keaktifan-masa bagi radioisotop Kalium-42. Radioisotop ini memancarkan zarah beta dan digunakan sebagai penyurih untuk mengukur kandungan garam dalam badan manusia.

  1. Nyatakan satu ciri-ciri zarah beta. [1 markah]
    Bercas negatif
  2. Berdasarkan Rajah 3, tentukan separuh hayat kalium-42. Tunjukkan kepada graf bagaimana anda menentukan separuh hayat bagi kalium-42.
    12 jam
  3. Berdasarkan separuh-hayat itu, nyatakan mengapa Kalium-42 sesuai digunakan sebagai penyurih. 
    Kalium-42 mempunyai setengah hayat yang pendek, maka dedahan yang berlebihan tidak berlaku.
  4. Hitung masa yang diambil bagi radioisotop Kalium-42 berkurang menjadi \(\frac{1}{8}\) daripada keaktifan asalnya. [2 markah]
    \(1 \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{2} \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{4} \underset{ T _{\frac{1}{2}}}{\longrightarrow} \frac{1}{8}\)
    Masa yang diambil untuk aktiviti kaliun-42 menjadi \(\frac{1}{8}\) daripada aktiviti asalnya.
    \[
    \begin{aligned}
    &=3 T _{\frac{1}{2}} \\
    &=3 \times 12 \text { jam }  \\
    &=36 \text {jam } 
    \end{aligned}
    \]



Soalan Berstruktur – Ayunan dan Perlembapan.

by

Rajah \(2.1\) menunjukkan sebuah spring berbeban berayun secara menegak di dalam air. Sistem ayunan itu mengalami pelembapan.
Rajah \(2.2\) menunjukkan graf sesaran-masa untuk sistem ayunan itu.

(a) Garis jawapan yang betul dalam kurungan untuk melengkapkan ayat di bawah. 

Pelembapan adalah suatu situasi apabila (amplitud, panjang gelombang) ayunan berkurang. [1 markah]

amplitud

(b) Nyatakan satu sebab mengapa pelembapan berlaku pada sistem ayunan itu. [1 markah]

Tenaga hilang disebabkan oleh geseran.

(c) Berdasarkan Rajah \(2.2\),
(i) nyatakan tempoh bagi sistem ayunan itu. [1 markah]

0.4s

(ii) berapakah frekuensi bagi sistem ayunan itu? [1 markah]

\(\begin{aligned} f &=\frac{1}{0.4} \\ &=2.5 Hz \end{aligned}\)

(d) Apakah yang akan berlaku kepada tempoh bagi sistem ayunan itu apabila beban yang lebih berat digunakan?

Bertambah

Hukum Kegravitian Semesta Newton

by

Hukum Kegravitian Semesta Newton

Daya Graviti Antara Dua Jasad dalam Alam Semesta

  1. Daya graviti ialah daya tarikan yang wujud di antara semua objek di alam semesta.
  2. Rajah di atas menunjukkan dua objek berjisim \(m_{1}\) dan \(m_{2}\). Jarak pemisahan antara dua objek itu ialah \(r .\) dan daya graviti yang bertindak antara dua objek ditanda\(F\).
  3. Menurut Hukum Kegravitian Semesta Newton, daya graviti, \(F\) antara dua objek itu adalah berkadar terus dengan hasil darab jisim kedua-dua objek. Iaitu
    \[
    F \propto m_{1} \times m_{2} \ldots \ldots \ldots \text { (1) }
    \]
  4. Daya graviti, \(F\) ini juga berkadar songsang dengan kuasa dua jarak antara pusat objekobjek tersebut.
    \[
    F \propto \frac{1}{r^{2}} \ldots \ldots \ldots \text { (2) }
    \]
  5. Menggabungkan (1) dan (2), kita akan dapati bahawa
    \[
    F \propto \frac{m_{1} \times m_{2}}{r^{2}}
    \]
    Maka,
    \[
    F=G \frac{m_{1} \times m_{2}}{r^{2}}
    \]
    di mana \(G=\) pemalar kegravitian semesta
    \[
    =6.67 \times 10^{-11} Nm ^{2} kg ^{-2}
    \]
  6. Formula ini merupakan formula bagi Hukum Kegravitian Semesta Newton.

Daya Dalam Keseimbangan

by

Vektor-vektor Dalam Keseimbangan


When 3 vectors are in equilibrium, the resultant vector = 0. After joining all the vectors tail to head, the head of the last vector will join to the tail of the first vector.
Apabila 3 vektor dalam keseimbangan, vektor paduannya = 0. Apabila melukis gambarajah vektor dengan  mengabungkan ekor satu vektor kepada kepala vektor yang lain, satu segitiga akan terbentuk.

Daya-daya Dalam Keseimbangan

Daya-daya dalam keseimbangan bermakna daya paduan dalam semua arah adalah sifar.
Jika daya-daya yang dikenakan ke atas satu objek adalah seimbang, mereka menghapuskan antara satu sama lain. Oleh itu, daya bersihnya ialah sifar.


Kesan :
  • Objek pegun tetap pegun [halaju = 0]
  • Objek bergerak akan terus bergerak dengan halaju malar [ pecutan = 0]

Contoh:

Rajah di atas menunjukkan satu beban berjisim 500g digantung oleh benang C. Benang C pula diikat kepada 2 benang A dan B. Cari tegangan benang A.

Jawapan:

Tegangan benang C, TC = berat beban = 5N.
Semua daya adalah dalam keseimbangan, maka,

Komponen menegak tegangan A = TC
TAcos60o = TC
TA = TC/cos60o
TA = 5/cos60o = 10N


External Link


Interactive Animation
Newton’s third Law of Motion – Java Applet

Leraian Daya

by

Leraian Vektor

  1. Satu vektor boleh dileraikan kepada dua komponen yang arahnya berserenjang antara satu sama lain.
  2. Biasanya dua komponen ini ialah
    1. komponen mengufuk
    2. komponen menegak
  3. Sama seperti kaedah segi empat selari vektor, kedua-dua komponen ini boleh digambarkan dalam gambar rajah leraian vektor seperti ditunjukkan di bawah.

Contoh:

Rajah di atas menunjukkan sebuah lori sedang menarik sebatang kayu balak dengan kabel besi. Jika tegangan pada kebel ialah 3000N dan daya geseran di antara kayu balak dan lantai ialah 500N, cari daya mengufuk yang dikenakan ke atas kayu balak itu.

Jawapan:
Komponen mengufuk daya tegangan pada kabel = 3000 cos30° =2598N
Geseran = 500N

Paduan daya mengufuk = 2598N – 500N =2098N

Contoh:

Rajah di atas menunjukkan dua daya bermagnitud 25N dikenakan ke atas satu objek berjisim 2kg. Cari pecutan objek itu dalam unit ms-2.

Jawapan:
Komponen mengufuk kedua-dua daya = 25cos45° + 25cos45° = 35.36N

Komponen menegak kedua-dua daya = 25sin45° – 25sin45° = 0N

Oleh itu, daya bersih yang dikenkan ke atas obejk itu = 35.36N

Pecutan objek boleh ditentukan daripada persamaan

F = ma
(35.36) = (2)a
a = 17.68 ms-2

External Link

Interactive Animation